Chapter 9.1 - 9.4 표준통제집단합성법

Chapter 9.1 - 9.4 표준통제집단합성법#

작성자: 김상돈

통제 집단 합성법이란?#

가상의 통제 집단을 생성하여 인과 효과를 측정하는 방법
- 처치가 없을 때의 시험군(\(E[Y_0|D = 1]\))과 비슷한 가상의 대조군(synthetic control)을 만드는 방법
패널 데이터 분석에 널리 활용됨

예제를 통해 문제를 다시 이해해보겠습니다.

온라인 마케팅 데이터셋

app_download(\(Y)\) : 일별 앱 다운로드 수
treated(\(D)\) : 마케팅 캠페인 집행 여부
city : 도시
Population : 도시의 인구
state : 주(보조 정보)
post : 개입 여부(\(I(t > T_{pre})\) )

데이터에 대한 특이 사항으로 treated ==1인 도시는 3개, treated ==0인 도시는 47개로 불균형합니다.

각 도시별 일별 앱 다운로드 수의 시계열 추이를 시각화해보겠습니다. treated ==1인 도시는 3개의 평균 결과(\(E[Y|D = 1]\))은 진한 선이고, 나머지 47개 도시는 연한 회색 선입니다. 5월 1일이 개입을 구분하는 시점입니다.

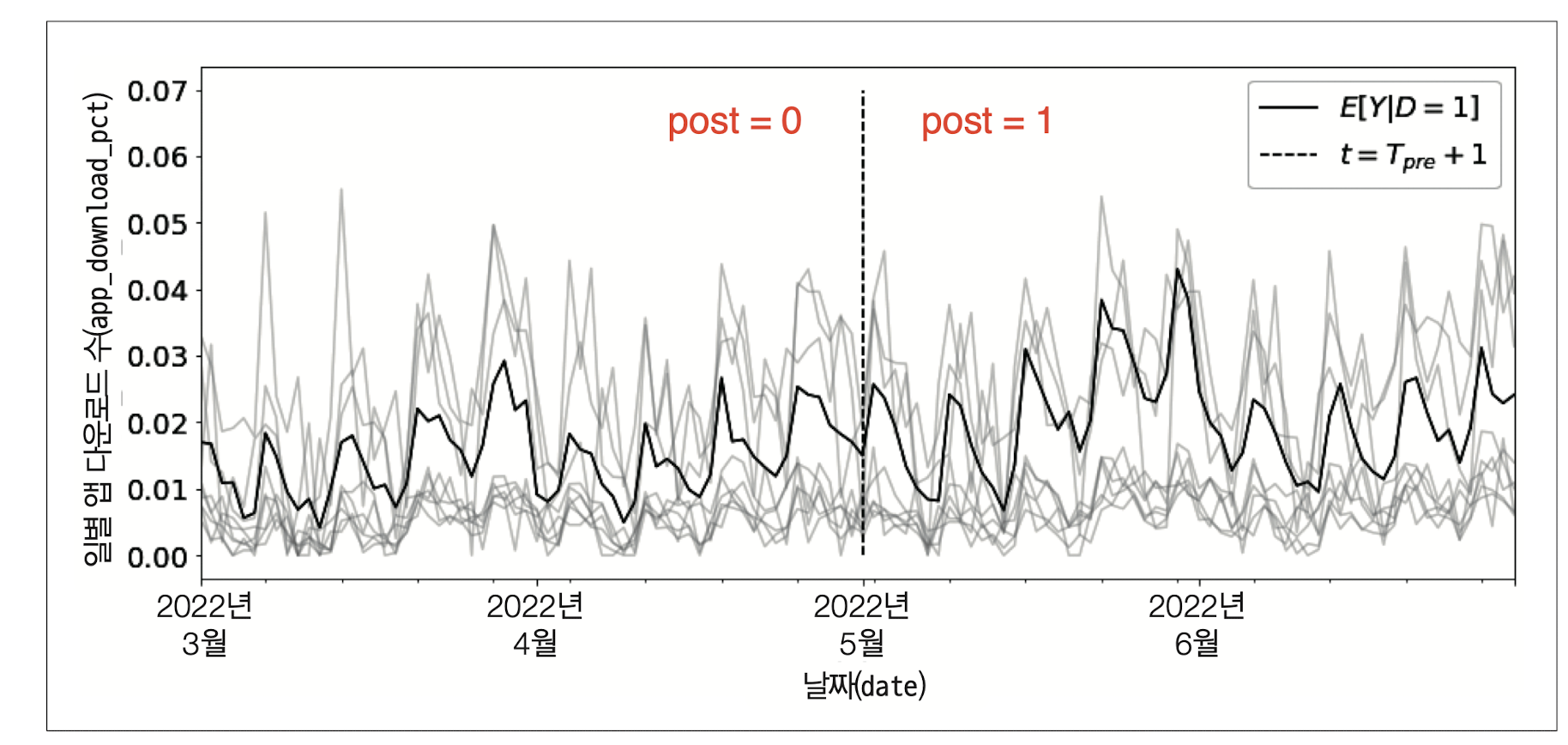
\(E[Y|D = 1]\)는 증가하는 형태를 보입니다. 단순 추세가 아닌 인과 효과를 계산하기 위해 ATT를 추정해보겠습니다.

\[ ATT = E[Y \mid D=1, \, \text{Post}=1] - E[Y_0 \mid D=1, \, \text{Post}=1] \]

\(ATT\)를 계산하기 위해서, \(E[Y \mid D=1, \, \text{Post}=1]\)는 구할 수 있지만, \(E[Y_0 \mid D=1, \, \text{Post}=1]\)는 구할 수 없습니다. 따라서 과거의 정보를 이용하여 \(E[Y_0 \mid D=1, \, \text{Post}=1]\)를 정확히 추정해야 합니다.

이 때 활용할 수 있는 방법이 통제집단합성법입니다.

이중 차분법과 통제집단합성법 비교#

	Difference-in-Differences (DID)	Synthetic Control Method
가정	평행 트렌드 가정, 처치에 대한 비기대 가정, 파급효과 없음	처치에 대한 비기대 가정, 파급효과 없음
장점	단순성과 직관적인 활용	맞춤형 통제 집단, 평행 트렌드 가정 불필요
단점	평행 트렌드 가정의 민감성, 외생적 사건의 영향	복잡성, 데이터 요구
적용 시기	평행 트렌드 가정 만족시	처리 집단과 통제 집단의 경향이 명확히 다를 때

가상의 통제집단과 수평 회귀#

통제집단합성법은 개입 이전 기간 정보를 활용하여 모형을 적합한 후, \(E[Y_0|D = 1]\)을 추정하는 것입니다. 즉, 해당 문제를 아래 아래 수식으로 정의할 수 있습니다.

개입 이전 시점의 정보를 활용하여 가중치를 구합니다.

\[ \hat{\omega}^{sc} = \arg\min_{\omega} \left\| \bar{Y}_{pre,tr} - Y_{pre,co} \omega_{co} \right\|^2 \]

\(\hat{\omega}^{sc}\)를 구하고, 개입 이후 시점의 결과(\(Y_{post, co}\))를 곱하면 \(E[Y_0|D = 1, Post = 1]\)를 추정할 수 있습니다. 수식의 꼴이 선형회귀모형에서 회귀계수를 구하는 수식과 유사하죠? 예시를 위해 선형회귀모형을 통해 통제집단합성법을 이해해보겠습니다.

y_pre_co : 5월 1일 이전 시점의 treat ==0인 47개 주의 일별 앱 다운로드 수

y_pre_tr : 5월 1일 이전 시점의 treat ==1인 3개 주의 일별 앱 다운로드 수 평균

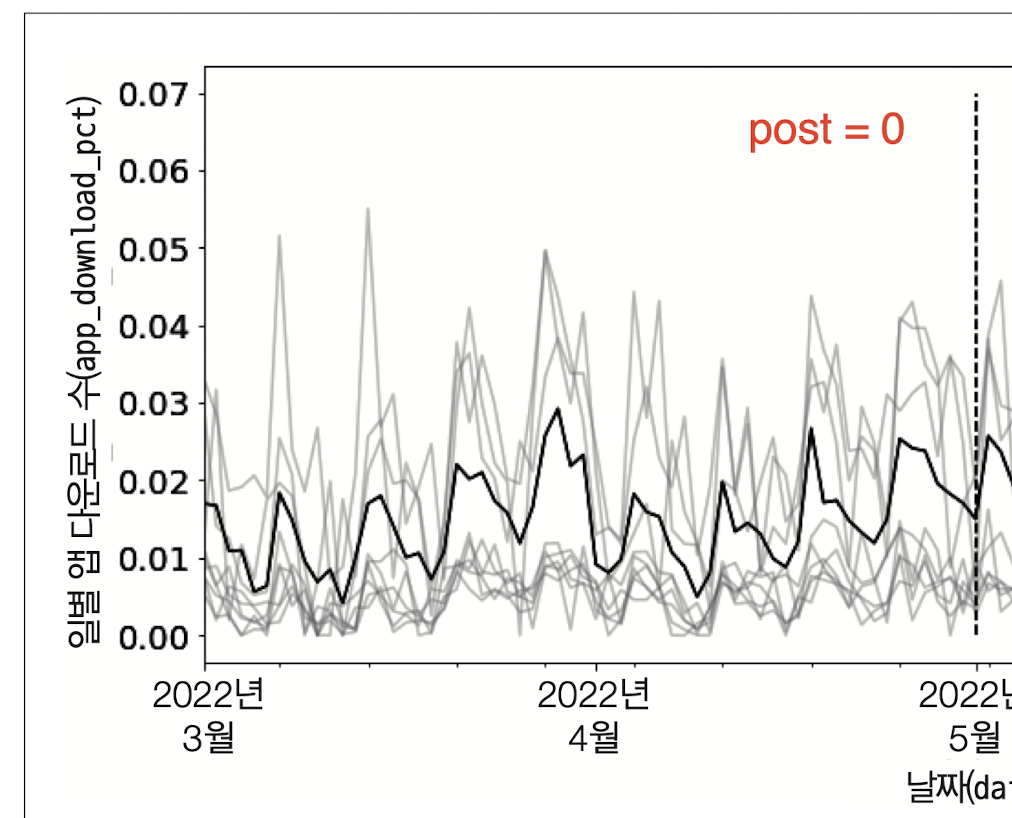
개입 이전 시점의 정보를 활용하여 선형회귀모형을 적합하겠습니다.

from sklearn.linear_model import LinearRegression

model = LinearRegression(fit_intercept=False)
model.fit(y_pre_co, y_pre_tr.mean(axis=1))
# extract the weights
weights_lr = model.coef_
weights_lr.round(3)

array([-0.65 , -0.058, -0.239,  0.971,  0.03 , -0.204,  0.007,  0.095,
        0.102,  0.106,  0.074,  0.079,  0.032, -0.5  , -0.041, -0.154,
       -0.014,  0.132,  0.115,  0.094,  0.151, -0.058, -0.353,  0.049,
       -0.476, -0.11 ,  0.158, -0.002,  0.036, -0.129, -0.066,  0.024,
       -0.047,  0.089, -0.057,  0.429,  0.23 , -0.086,  0.098,  0.351,
       -0.128,  0.128, -0.205,  0.088,  0.147,  0.555,  0.229])

개입 이전 정보를 활용하여 \(\hat{\omega}^{sc}\)를 구했으므로, 5월 1일 이후 시점(post = 1)의 \(E[Y_0|D = 1, Post = 1]\)를 추정할 수 있습니다. Post = 0, Post =1인 전체 시점의 시계열 추이를 그리면 다음과 같습니다.

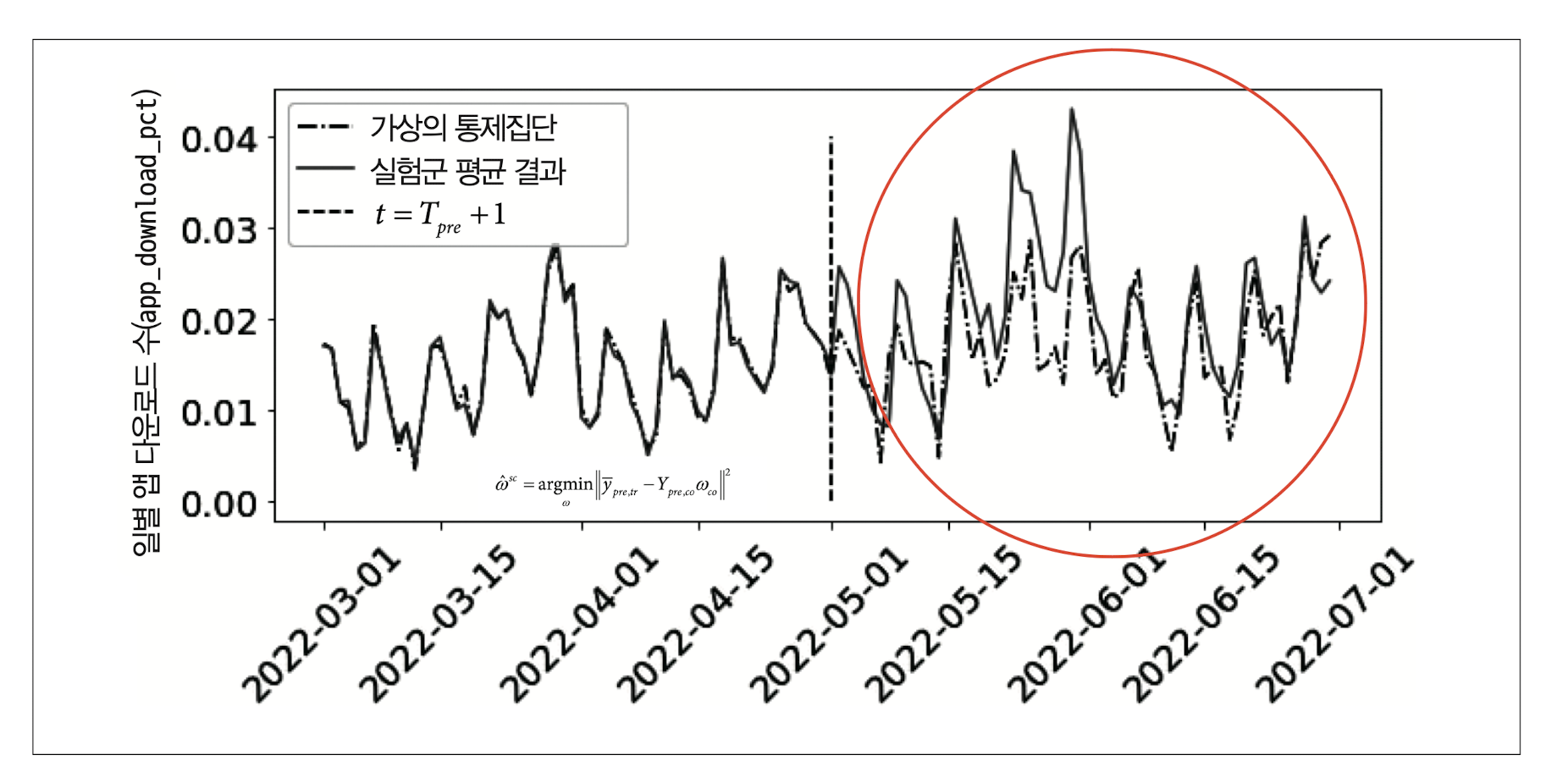
그림을 통해 보면 대체로 \(E[Y \mid D=1, \, \text{Post}=1] > \hat{E}[Y_0 \mid D=1, \, \text{Post}=1]\)이므로, 온라인 마케팅 캠페인은 긍정적인 효과를 가져왔음을 알 수 있습니다. ATT 추정 결과를 시각화해보겠습니다.

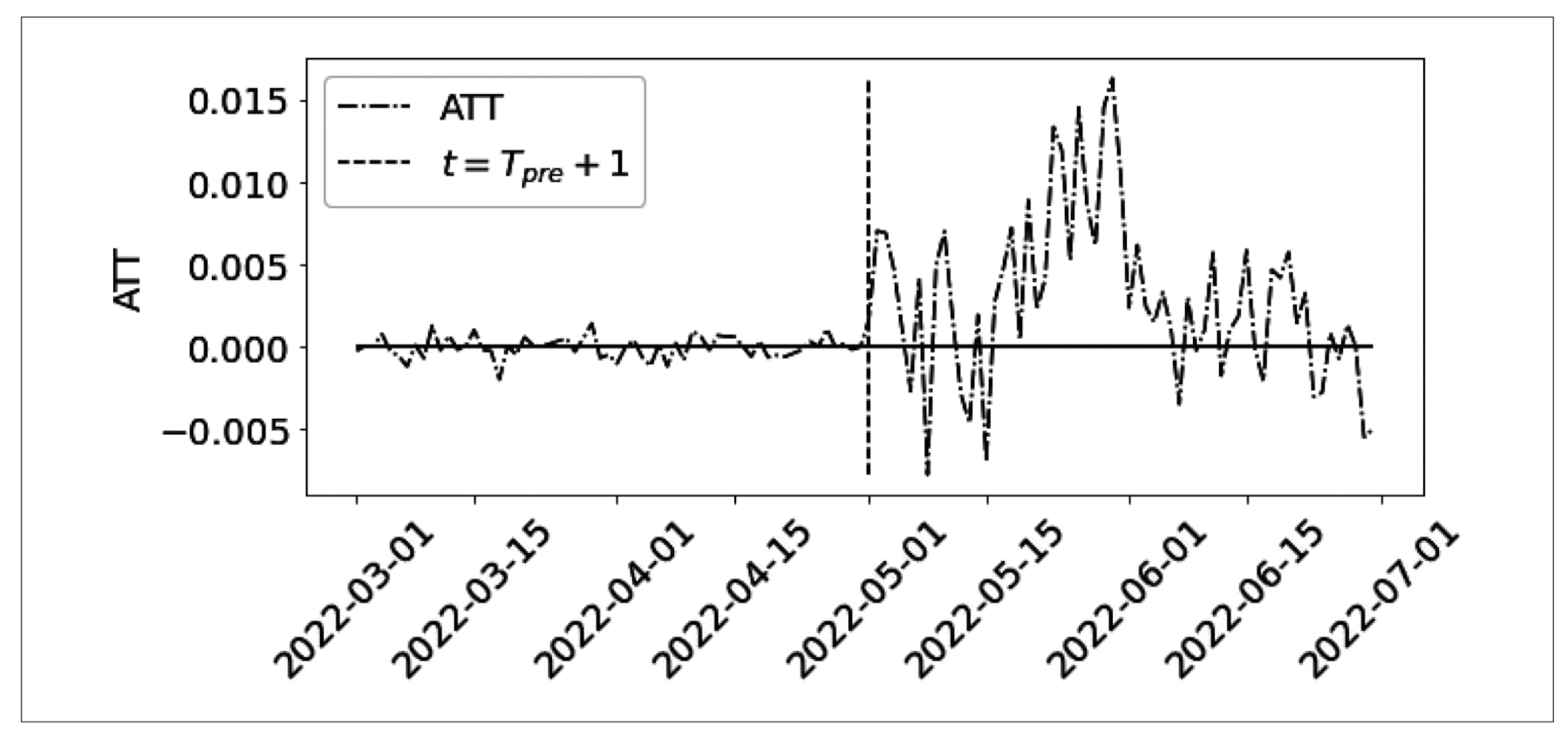
효과가 점진적으로 증가하다가, 점차 감소하는 것을 확인할 수 있습니다. 광고 효과가 나타나기까지 시간이 걸리므로 이러한 점진적 증가가 종종 관측됩니다. 마케팅에서는 novelty effect라고 표현합니다.

개입 이전 시점의 잔차가 매우 작은 것을 확인할 수 있습니다. 이는 선형회귀모형의 과적합이 의심되며, \(\hat{E}[Y \mid D=1, \, \text{Post}=1] > \hat{E}[Y_0 \mid D=1, \, \text{Post}=1]\) 결과를 신뢰할 수 없게 됩니다.

보통 통제집단합성법에서는 단순한 선형회귀모형보다는 제약조건을 추가하여 활용합니다.

표준 가상의 통제집단#

표준 가상의 통제집단 공식은 다음과 같은 제약 조건을 추가합니다.

\[\begin{split} \hat{\omega}^{sc} = \arg\min_{\omega} \left\| \bar{Y}_{pre,tr} - Y_{pre,co} \omega_{co} \right\|^2 \\\text{s.t.} \quad \sum_i \omega_i = 1 \quad \text{and} \quad \omega_i > 0 \quad \forall i \end{split}\]

QP programming

원래의 QP 문제를 다음과 같이 변환할 수 있습니다:

\[ \hat{\omega}^{sc} = \arg\min_{\omega} \left\| \bar{Y}{pre,tr} - Y{pre,co} \omega_{co} \right\|^2 \]

제약 조건:

\[\begin{split} C\omega = d \quad \text{where} \quad C = [1, 1, \ldots, 1], \quad d = 1 \\ A\omega \leq b \quad \text{where} \quad A = -I, \quad b = 0 \end{split}\]

따라서, 최종 형태는 다음과 같습니다:

\[ \hat{\omega}^{sc} = \arg\min_{\omega} \left\| \bar{Y}{pre,tr} - Y{pre,co} \omega_{co} \right\|^2 \quad \text{s.t.} \quad C\omega = d \quad \text{and} \quad A\omega \leq b \]

이 형태는 일반적인 Quadratic Programming 문제의 형태를 충족합니다.

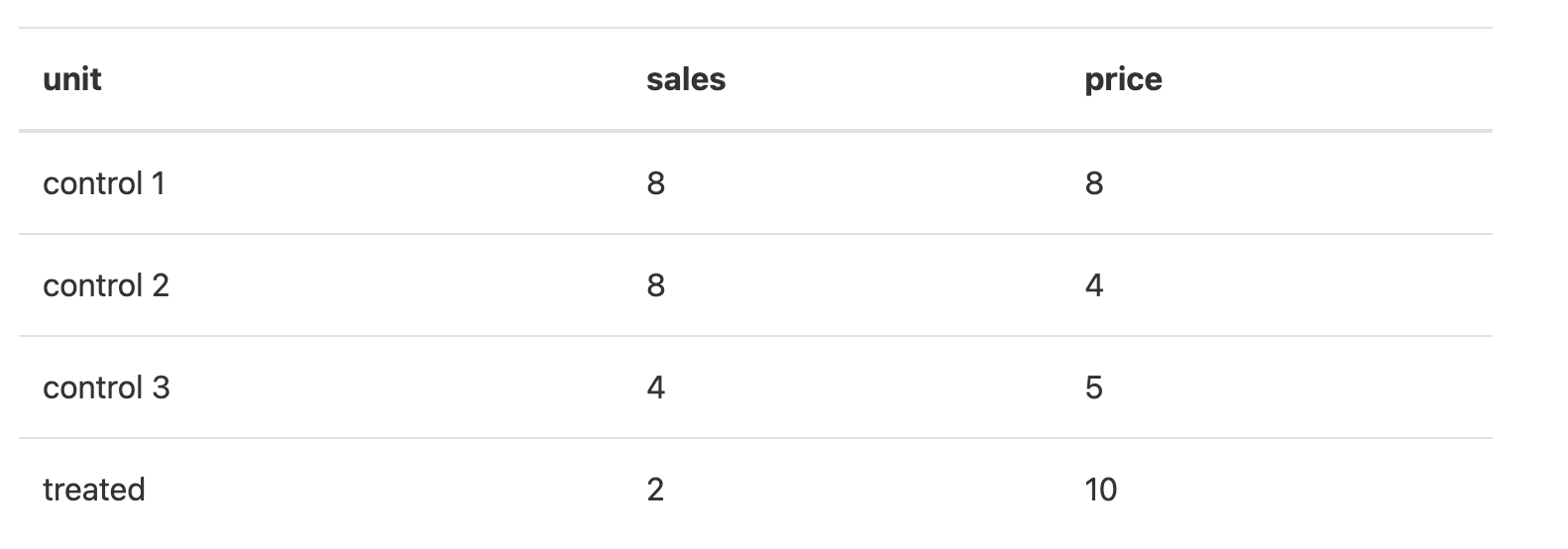
제약 조건을 추가하는 이유는 첫 번째로, 외삽을 방지함으로써 과적합을 방지합니다(아래 그림 참고).

https://causalinferencelab.github.io/Causal-Inference-with-Python/15-Synthetic-Control.html

예를 들어, control 1에는 가중치 2.25를 곱하고, control 2에는 가중치 -2를 곱한다고 해보겠습니다. control 2의 경우 음수 가중치를 곱하게 되므로, 매출(sales), 가격(price)는 음수가 됩니다. 매출과 가격은 음수가 될 수 없으므로, 의미 없는 데이터의 영역을 추정하게 됩니다.

두 번째로, 해석 가능성입니다.

제약 조건 1: \(\sum_i \omega_i = 1\)

제약 조건 2 : \(\omega_i >0\)

제약 조건을 설정할 경우 \(\hat{E}[Y \mid D=1, \, \text{Post}=1] > \hat{E}[Y_0 \mid D=1, \, \text{Post}=1]\)를 추정하는데 중요하지 않은 가중치 대부분은 0이 됩니다. 또한, 가중치의 합이 1이므로, 가상의 통제집단을 생성하는데 필요한 각 단위들의 기여도 관점에서 해석해볼 수 있습니다.

제약식이 존재하는 QP 프로그래밍이므로, 파이썬에 구현된 최적화 패키지인 cvxpy를 활용하여 \(\hat{\omega}^{sc}\) 를 구해보겠습니다.

model = SyntheticControl()
model.fit(y_pre_co, y_pre_tr.mean(axis=1))

# extrac the weights
model.w_.round(3)
array([-0.   , -0.   ,  0.   , -0.   , -0.   , -0.   ,  0.084,  0.039,
        0.085,  0.003, -0.   , -0.   , -0.   , -0.   , -0.   ,  0.   ,
        0.062,  0.121, -0.   ,  0.072, -0.   ,  0.   , -0.   ,  0.   ,
       -0.   , -0.   ,  0.   , -0.   , -0.   ,  0.   , -0.   ,  0.095,
        0.   , -0.   ,  0.   ,  0.022,  0.116, -0.   ,  0.068,  0.046,
       -0.   , -0.   , -0.   ,  0.088,  0.   ,  0.098, -0.   ])

가중치 \(\hat{\omega}^{sc}\)는 모두 0 이상인 것을 확인할 수 있습니다. 가중치를 구했으므로, \(\hat{E}[Y \mid D=1, \, \text{Post}=1] > \hat{E}[Y_0 \mid D=1, \, \text{Post}=1]\)와 ATT를 시각화해보겠습니다.

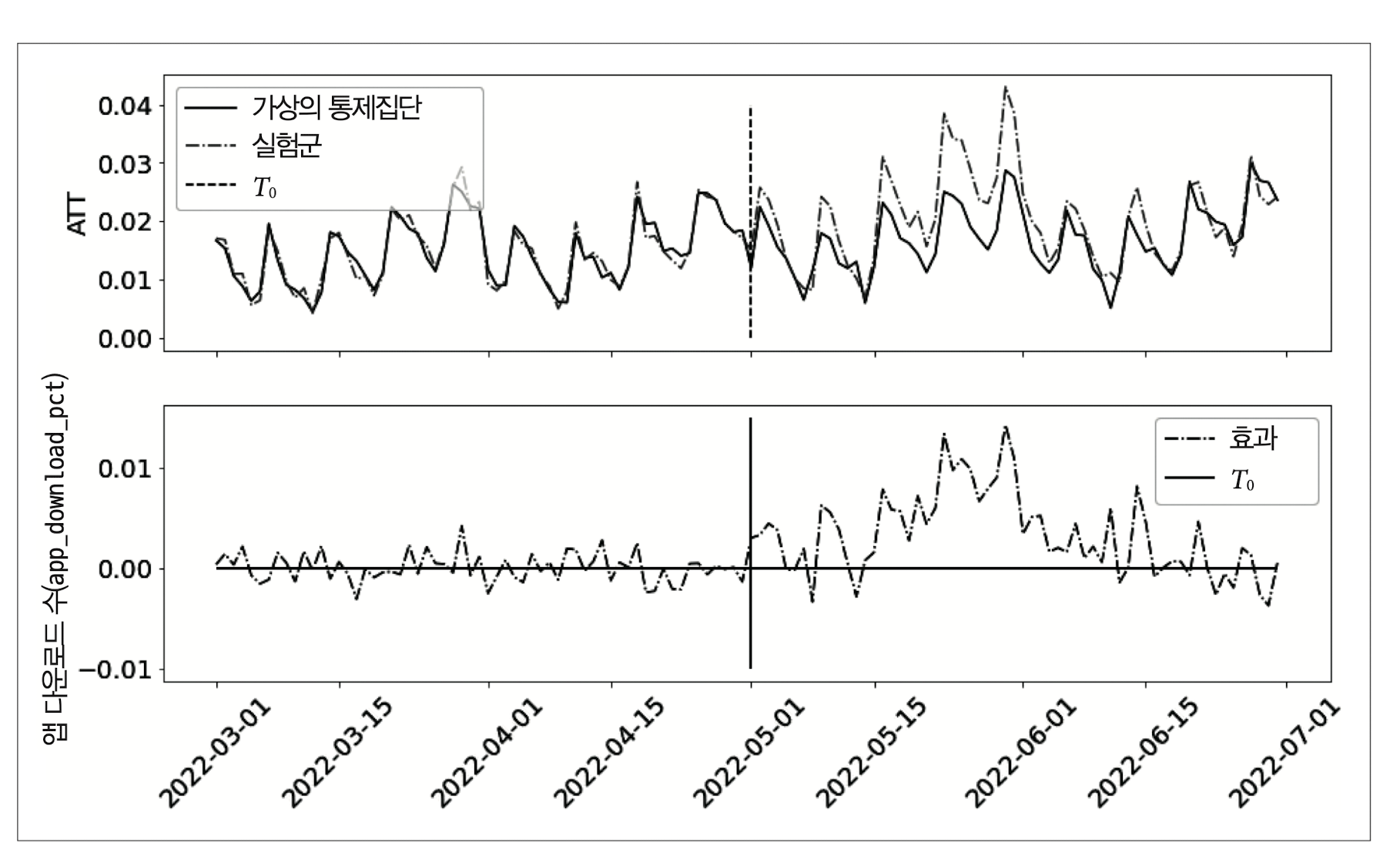
ATT의 경우 제약식이 없는 선형회귀모형을 적합했을 때에 비해 개입 전 모델의 잔차는 커졌지만, ATT는 추세는 이전과 비슷하지만 잡음이 줄어든 것을 확인할 수 있습니다. 즉, 과적합을 방지함으로써 일반화 성능이 더 높아진 것을 확인할 수 있습니다.