Chapter 11.1-11.6 불응과 도구변수#

작성자 : 하소희

개념#

불응#

  • 요구나 요청에 응하지 않음

  • 처치를 배정 받은 모든 사람이 처치 받지 않음을 의미

    • 즉, 처치가 배정되었다고 처치가 반드시 적용되지 않을 수 있음을 의미

  • 처치 여부를 무작위로 결정하더라도 고객이 이를 선택할 수 있는 상황에서 발생

도구변수#

  • 불응과 같은 문제에서 처치가 결과에 미치는 인과 효과를 정확히 추정하기 위한 방법

  • 도구변수는 처치와 관련이 있고 결과 변수와 직접적인 관련이 없어야 함

처치 배정과 처치 적용에 따른 4가지 그룹#

  • 순응자: 자신에게 배정된 처치 받는 사람

  • 항시 참여자: 배정과 관계 없이 항상 처치 받는 사람

  • 항시 불참자: 배정과 관계없이 처치를 한 번도 받지 않은 사람

  • 반항자: 배정된 처치와 반대되는 처치 받는 사람

불응 DAG#

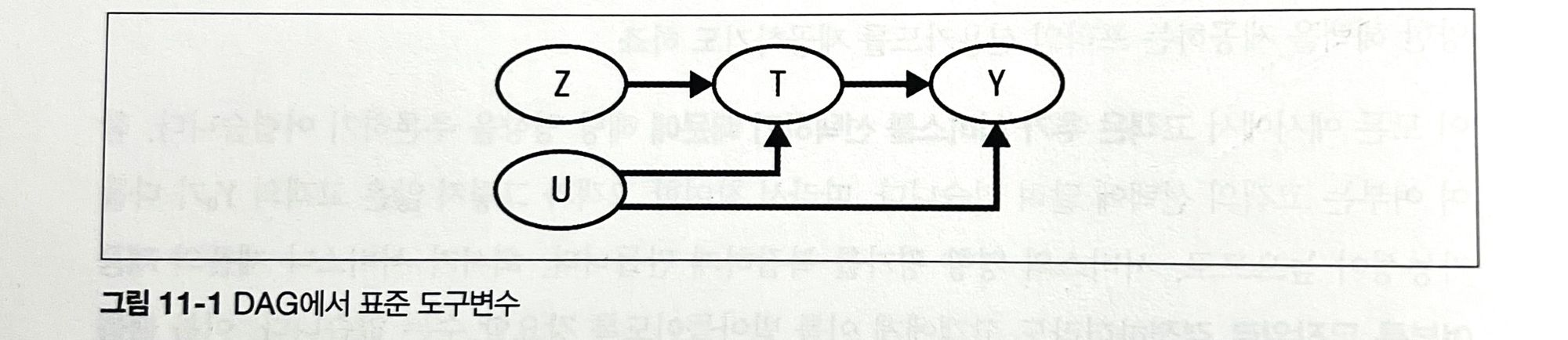
  • Z : 도구변수

      1. 교란 없이 처치에 영향을 주고

      1. 처치를 거치지 않으면 결과에 영향을 미치지 않는 변수

  • T : 처치

  • Y : 결과

  • U : 교란요인

불응에서 처치에 따른 효과를 정확히 판단할 수 없음

: U를 통과하는 열린 뒷문 경로 때문에 처치가 Y에 미치는 영향을 제대로 식별할 수 없기 때문

  • 열린 뒷문 경로 → 처치와 결과가 공통 원인을 공유하는 상황(U)

불응 예시#

  • Z : 프라임 신용카드 이용 가능 여부(무작위배정)

  • T : 프라임 카드 보유 여부

  • Y : 구매금액

  • U : 교란요인

ITTE ↔ ATE 비교#

처치 의도 효과(ITTE)#

  • Z는 무작위로 배정되기 때문에(예시에서) 단순 선형회귀로 추정가능

\[ ITTE = E[Y|Z =1]-E[Y|Z = 0] = E[Y_1,_t - Y_0,_t] \]

✅그러나 ITTE가 처치효과와 같다고 말할 수 없음

✅실제 처치를 받지 않은 대상자가 포함되기 때문에, 처치의 실제 효과를 과소평가할 수 있음

✅중요한 건 카드 선택(처치 받은 대상자)에 따른 처치효과를 파악하는 것

ITTE ↔ ATE 차이#

  • ITTE: 모든 배정된 대상을 포함하므로 실제 효과를 과소평가할 수 있음

  • ATE: 실제로 처치를 받은 대상자만 포함하여 더 정확한 처치 효과를 반영

✅ 따라서, 불응이 발생하면(무작위 처치 배정과 상관없이) 처치를 받은 사람과 받지 않은 사람이 혼재되어 있기 때문에 ITTE 추정값이 처치의 실제 효과를 과소평가하게 됨

✅ ITTE 추정값은 ATE 추정값보다 0에 가깝게 편향됨(처치의 효과가 0에 가까워짐을 의미)

처치 선택에 따른 ATE 식별 불가#

  • 불응 상태에서는 처치 선택이 무작위가 아니므로, 처치 받은 경우와 받지 않은 경우를 비교해도 ATE를 제대로 식별할 수 없음

✅ ITTE의 값은 대리 변수로 사용할 수 있지만, 처치의 실제 효과를 과소평가 하게 됨

✅ 처치 선택이 무작위가 아니기에 ATE를 제대로 식별할 수 없음

→ 추가적인 가정 필요

도구변수 식별 가정#

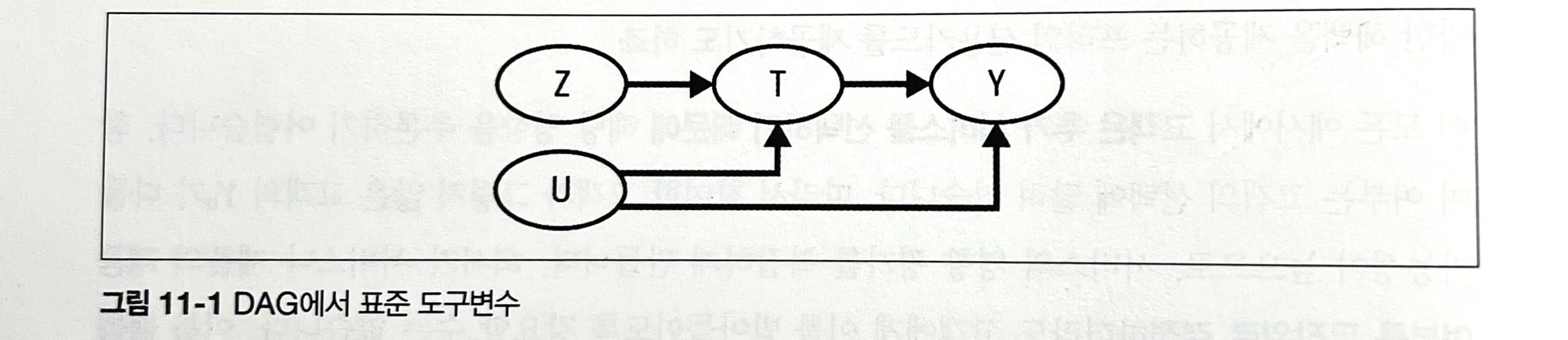
ITTE 에서 출발

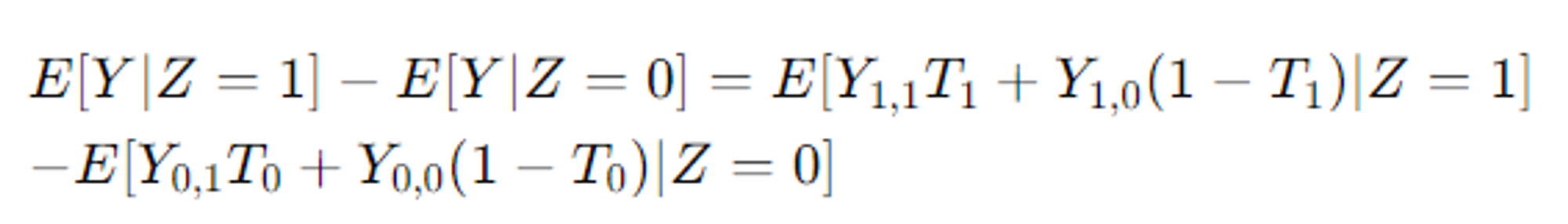
1. 연관성#

  • 도구변수가 처치변수에 영향을 미쳐야 함

2. 배제 제약#

  • 처치 T를 통하지 않고는 Z에서 Y로 가는 경로가 없다는 가정

  • 도구변수가 처치를 통해서만 결과에 영향을 미침

  • \(Y_z,_t = Y_t\)

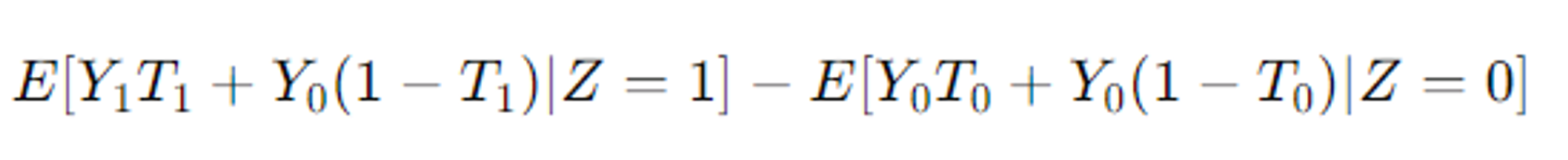
3. 독립성#

  • Z와 T 그리고 Z와 Y 사이에 측정되지않은 교란요인이 없다고 가정

  • 도구변수가 무작위로 배정된것처럼 작용

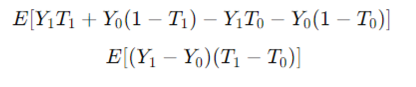
4. 단조성#

  • 도구변수가 처치변수를 한 방향으로만 영향을 주는 것을 의미

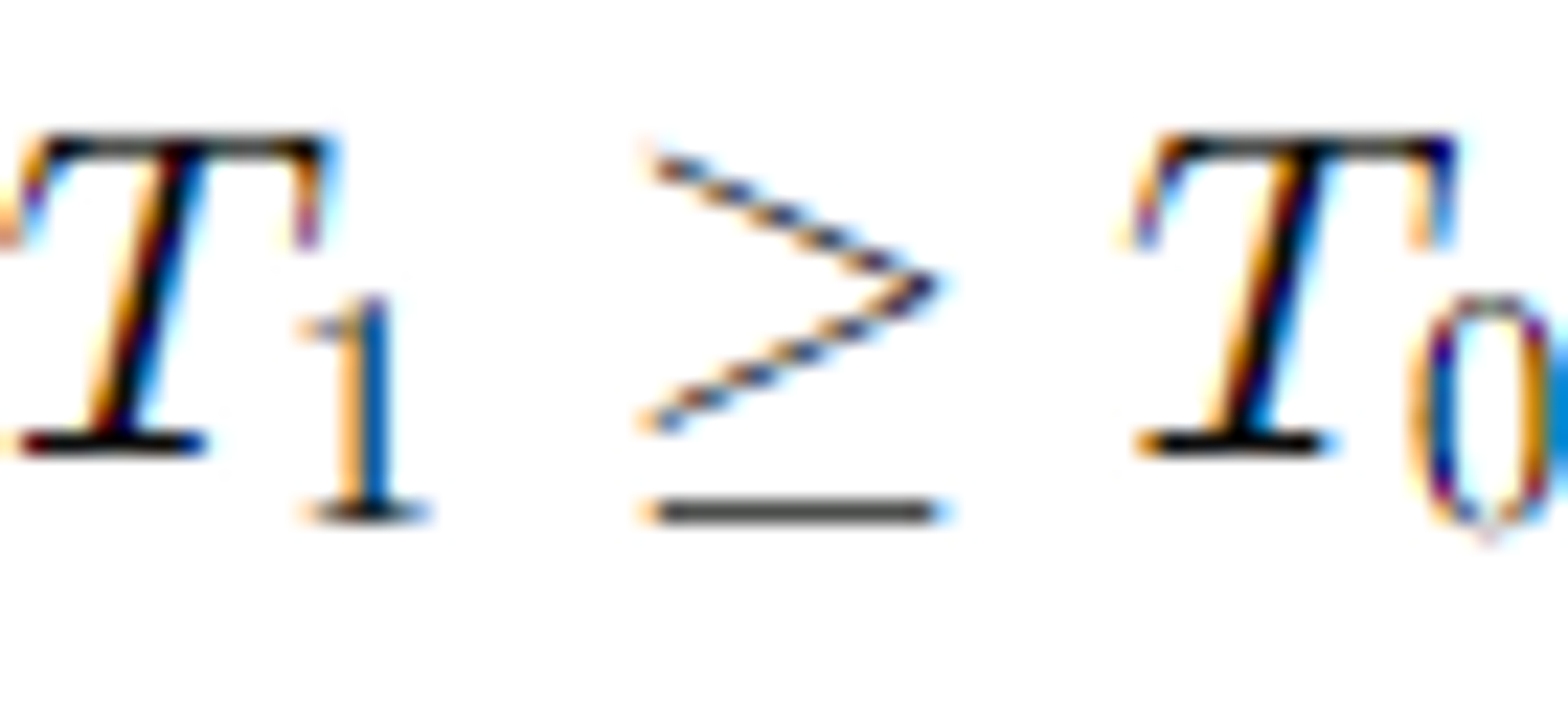
  • 참고

    \(T_1>T_0\)인 값을 갖는 그룹은 순응자 밖에 없음

    • 순응자(Complier) : 배정된 처치를 받는 사람들(T1=1, T0 = 0)

    • 항시 참여자 (Always-taker): 도구변수와 상관없이 항상 처치를 받는 사람들 (T1=1, T0=1).

    • 항시 불참자자 (Never-taker): 도구변수와 상관없이 처치를 받지 않는 사람들 (T1=0, T0=0).

    • 반항자 (Defier): 도구변수의 할당과 반대로 행동하는 사람들 (T1=0, T0=1).

결과#

\[ E[Y_1-Y_0|T_1>T_0] = \frac{E[Y|Z=1]-E[Y|Z=0]}{E[T|Z=1]-E[T|Z=0]} \]

도구변수 실습#

1단계#

  • 1단계 - 회귀: 처치 변수를 도구변수에 대해 회귀하는 단계 → 연관성 가정 확인 가능

  • 도구변수와 관련된 매개변수 추정값이 크고 통계적으로 유의 → 해당 가정이 유효

  • Z → T 추정

2단계#

  • 2단계 - 축약형 : 결과를 도구변수에 회귀하여 처치 의도 효과를 추정

  • Z → Y 추정

LATE = 2단계 추정값 / 1단계 추정값

2단계 최소제곱법#

  • 개념

    • 2단계에서 결과(Y)를 1단계에서 구한 T의 예측값(\(\hat{T}\))에 회귀하는 방법

  • 장점

    • 표준오차를 적절하게 계산할 수 있음

    • 더 많은 도구변수와 공변량을 추가할 수 있음