Chapter 2. 무작위 실험 및 기초 통계 리뷰#
Recap#
작성자 : 최의관
인과관계와 연관관계의 차이는 무엇인가?
→ 연관관계는 실험군에 대한 평균 처치 효과(ATT) 와 대조군과 실험군의 차이(편향)
→ 편향은 앞 Chapter 예로 설명하면 할인을 할 수 있는 여력을 가진 회사 규모 간의 차이
→ 즉, 편향이 0이면 연관관계는 인과관계가 된다
→ 대조군과 실험군은 교환 가능해야 한다
인과추론에서 독립성 가정이 중요하다.
처치와 결과 사이의 독립성을 이야기하는 것이 아닌, 처치와 잠재적 결과가 서로 독립이어야 한다.
처치 배정 시, 랜덤화 배정 진행으로 해결할 수 있다 (무작위 통제 실험 RCT)
RCT (Randomized Control Trial)#
RCT를 통해서 이론적으로는 독립성이 성립해야 하지만, 실제로는 반드시 그렇지 않다.
실험군과 대조군이 비슷한지 확인하기 위해서 정규화 차이(normalized difference)를 계산해 볼 수 있다.
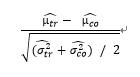
(μ_hat와 σ_hat는 표본 평균과 분산을 뜻함)
→ 정해진 임계값은 없지만 일반적으로 0.5 정도가 적절
→ 대규모 표본에서는 정규화 차이가 사라지는 경향이 있음
→ 우리는 RCT를 통해 독립성 가정을 만족하며 ‘식별’을 할 수 있음
추정#
인과추론은 크게 두 단계로 이루어진다.
‘식별’을 통해 관측할 수 없는 인과 추정량을 데이터에서 추정할 수 있는 관측 가능한 통계량으로 바꾼다.
다음 단계로는 그 통계량을 통해 ‘추정’ 을 해야 한다.
추정 과정에서 중요한 것은 ‘얼마나 부정확한가’에 대해 정량적으로 측정하는 것입니다.
그리고 그것은 **‘추정값의 분산’**을 통해 계산 가능
분산: 관측 값이 중심값(기댓값)에서 얼마나 벗어나 있는지 정도
분산은 관측한 데이터(표본)의 크기가 증가함에 따라 줄어듦
💡 데이터 불확실성 체계적 오차: 모든 측정값에 동일한 방식으로 영향을 미치는 일관된 편향 무작위 오차: 우연히 생긴 예측 불가능한 변동 → 체계적 오차는 줄일 수 없지만, 무작위 오차는 표본 수를 증가시킴으로써 줄일 수 있다
추정값의 표준오차 (Standard Error), 신뢰구간 (Confidence Interval)#

(SE : 평균의 표준오차, σ : 표준편차, n : 표본크기)
실험의 평균 값은 실제 평균과 항상 동일할 순 없지만, 표준오차를 사용해 진행하는 실험의 95%에서 실제 평균을 포함하는 구간을 만들 수 있다. → 신뢰구간
각 실험에서 95% 신뢰구간을 구성한다면 실제 평균이 100번 중 95번은 신뢰구간 내에 속함을 의미.
즉, ‘표본평균’ 분포의 표준편차가 표준오차(SE)이다.
따라서, 표준오차에 2를 곱하고 실험 평균에서 더하고 빼면 실제 평균에 대한 95% 신뢰구간을 구성할 수 있다.
각 그룹 간 95% 신뢰구간이 서로 겹치지 않는다면, 통계적으로 유의한 차이가 있다고 볼 수 있다.하지만, 반대로 구간이 겹친다고해서 그룹 간 차이가 통계적으로 유의하지 않다고 단정할 순 없다.
신뢰구간은 추정값에 대한 불확실성을 나타내는 방법이다. → 표본 크기가 작을수록 표준오차는 커지고, 그 결과 신뢰구간도 넓어진다
가설 검정 (Hypothesis Testing)#
불확실성을 나타내는 또 다른 방법은 가설검정을 통해 결과를 제시하는 것이다.
두 그룹 간 평균 차이가 통계적으로 유의한 차이가 있는지에 대한 물음에 답을 하기 위해서는 두 독립 정규분포의 합이나 차 역시 정규분포라는 점을 기억해야 한다.
정규분포의 합이나 차는 아래와 같은 분포를 따른다.
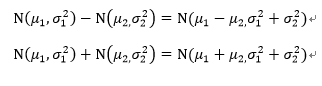
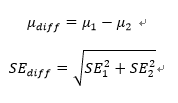
귀무 가설 (Null Hypothesis)#
귀무가설은 아래와 같이 설정할 수 있습니다.
\(H_0 : Conversion_{no-email} = Conversion_{short-email}\)
귀무가설: 두 그룹 간에 차이가 없다. → 두 그룹 간 차이의 신뢰구간을 측정하여, 그 신뢰구간 내 0을 포함하는지 아닌지 확인을 통해 두 그룹 간 차이가 유의한지 아닌지 확인할 수 있습니다.
0을 포함한다면, 평균 차이 값이 95% 신뢰 수준 아래 100번 중 95번은 신뢰구간 내에 0이 속함을 의미한다고 볼 수 있다.
반대로, 포함하지 않는다면 실험 100번중 95번은 신뢰구간 내에 0이 속하지 않음을 의미한다.
그렇다면 우리는 유의수준 a = 0.05 (95%신뢰도) 하에서 귀무가설을 기각할 수 있다.
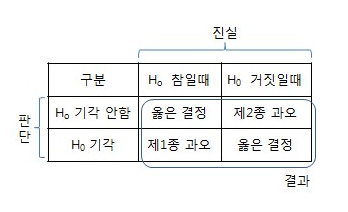
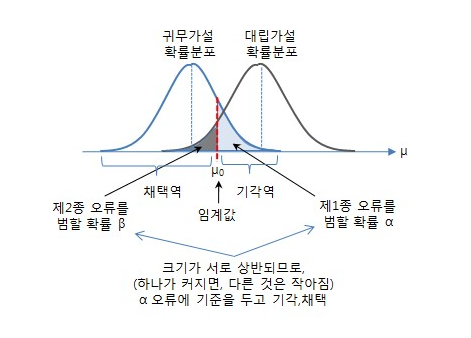
(출처: http://www.ktword.co.kr/test/view/view.php?m_temp1=5094)
※ 귀무가설을 꼭 두 그룹이 동등함을 전제로 설정되어야 하는 것은 아니다.
매개변수가 특정 값과 다른 경우를 귀무가설로 세워야 하는 경우도 있다.
검정 통계량 (Test Statistic)#
위에서 설명한 신뢰구간 외에도, 검정통계량을 사용하여 귀무가설을 기각할 수도 있다.
대체로 값이 클수록 귀무가설을 기각하는 방향으로 설정하게 된다.
가장 널리 사용하는 통계량 중 하나는 t-통계량이고, 신뢰구간을 형성하는 분포를 정규화함으로써 아래와 같이 정의된다.
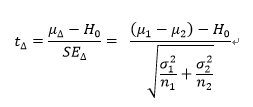
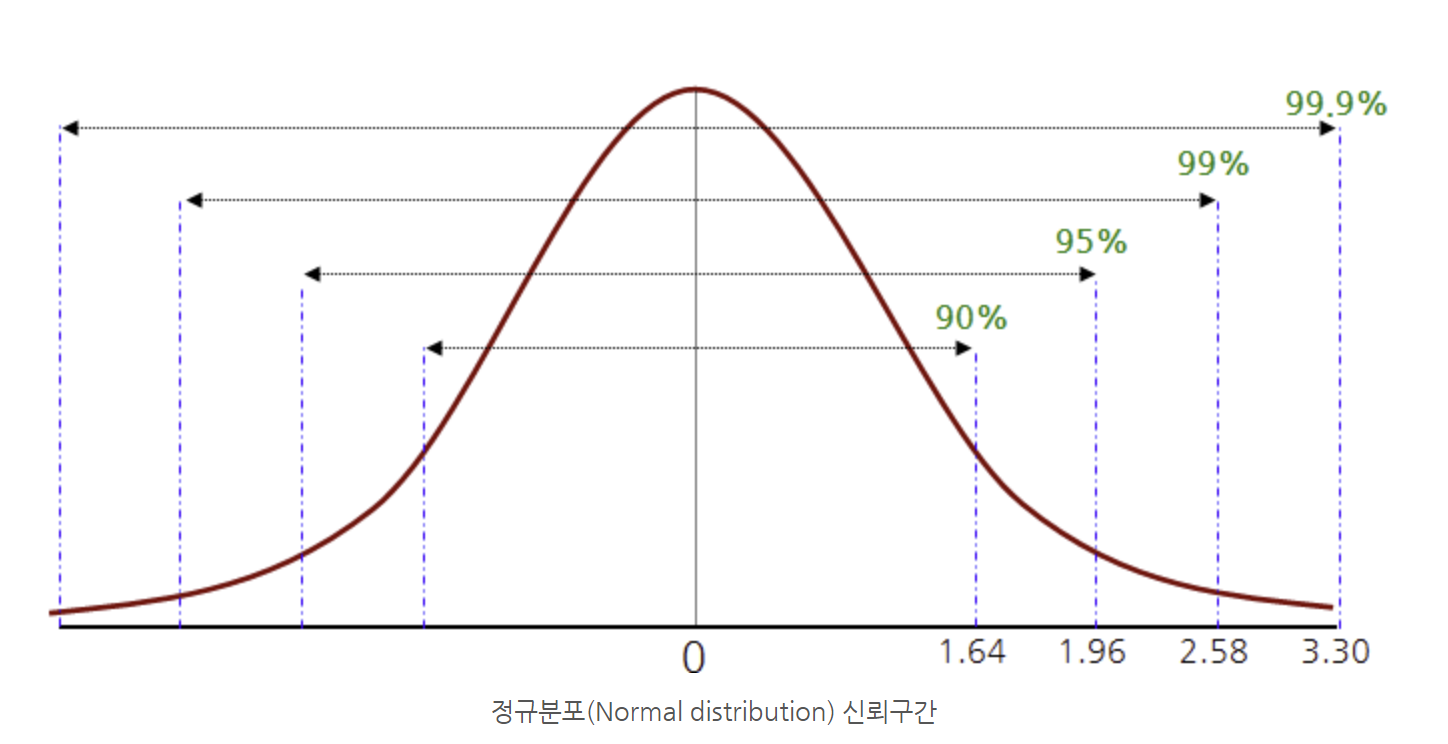
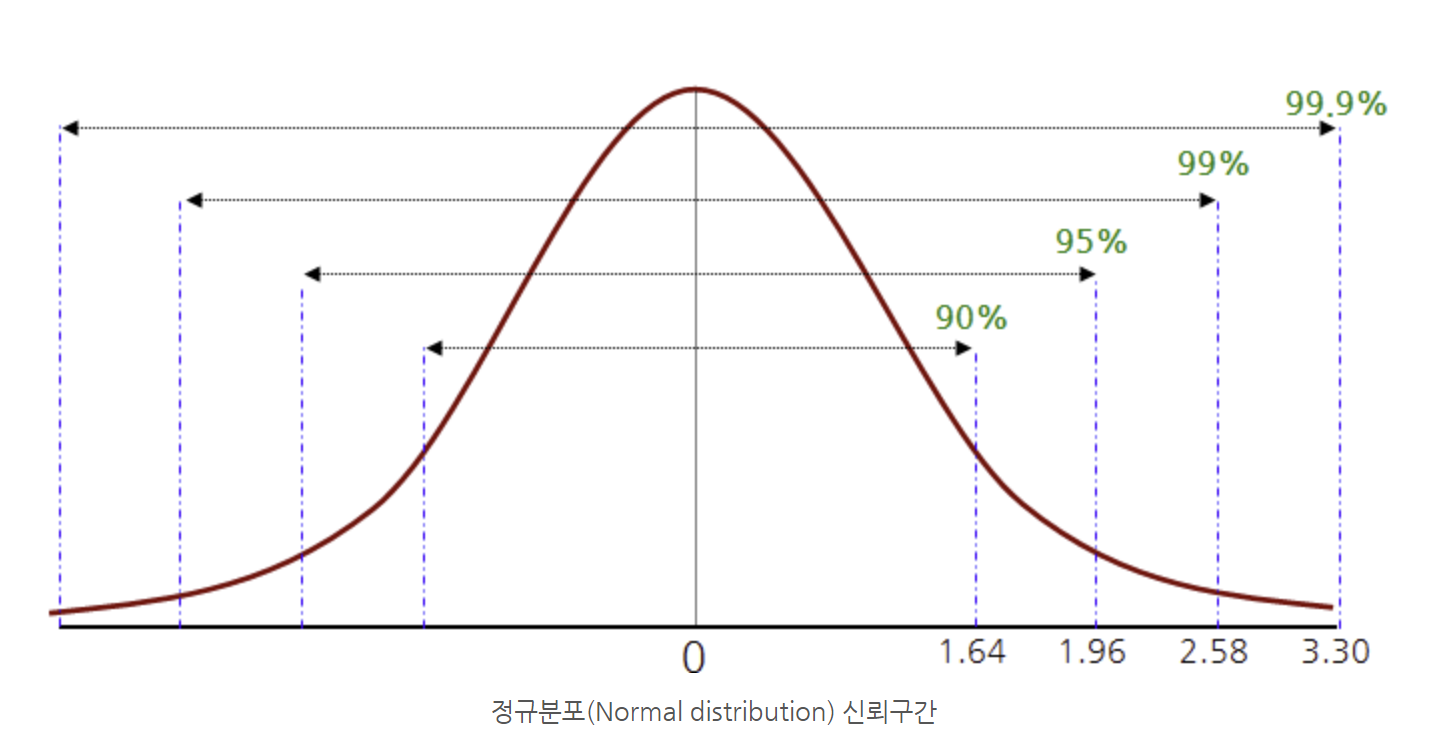
귀무가설이 참인 경우 위 통계량의 분포는 평균이 0이고 분산이 1인 정규분포를 따릅니다. (95%의 질량이 0을 중심으로 1.96과 -1.96 내에 형성 되어있습니다.)
통계량 값이 1.96보다 크거나 -1.96보다 작은 경우, 유의수준 5% 하에서 기각할 수 있습니다.
P 값 (P-Value)#
p-value가 작을수록 귀무가설이 틀렸을 가능성이 높아집니다.
일반적으로 p-value < 유의수준 α(보통 0.05 또는 0.01) → 귀무가설 기각, 대립가설을 채택.
반대로 p-value > 유의수준 α → 귀무가설 채택
표본 크기 계산#
표본계산 추가자료
실험을 설계할 때, 각 그룹에 표본을 최소 어느 정도 설정해야 하는지 중요하다.
귀무가설이 거짓일 경우 이를 정확하게 기각할 만큼 충분히 큰 표본을 확보해야 한다.
(표본이 작으면 추정량의 분산이 커지고, 분산이 커질수록 추정이 부정확하기 때문에 표본의 확보가 중요하다.)
95% 신뢰구간이란, 우리가 실험을 통해 얻은 신뢰구간 중 95%가 추정하고자 하는 매개변수의 실젯값을 포함함을 의미한다. 나머지 5%에서 실젯값을 포함하지 않음을 의미한다.
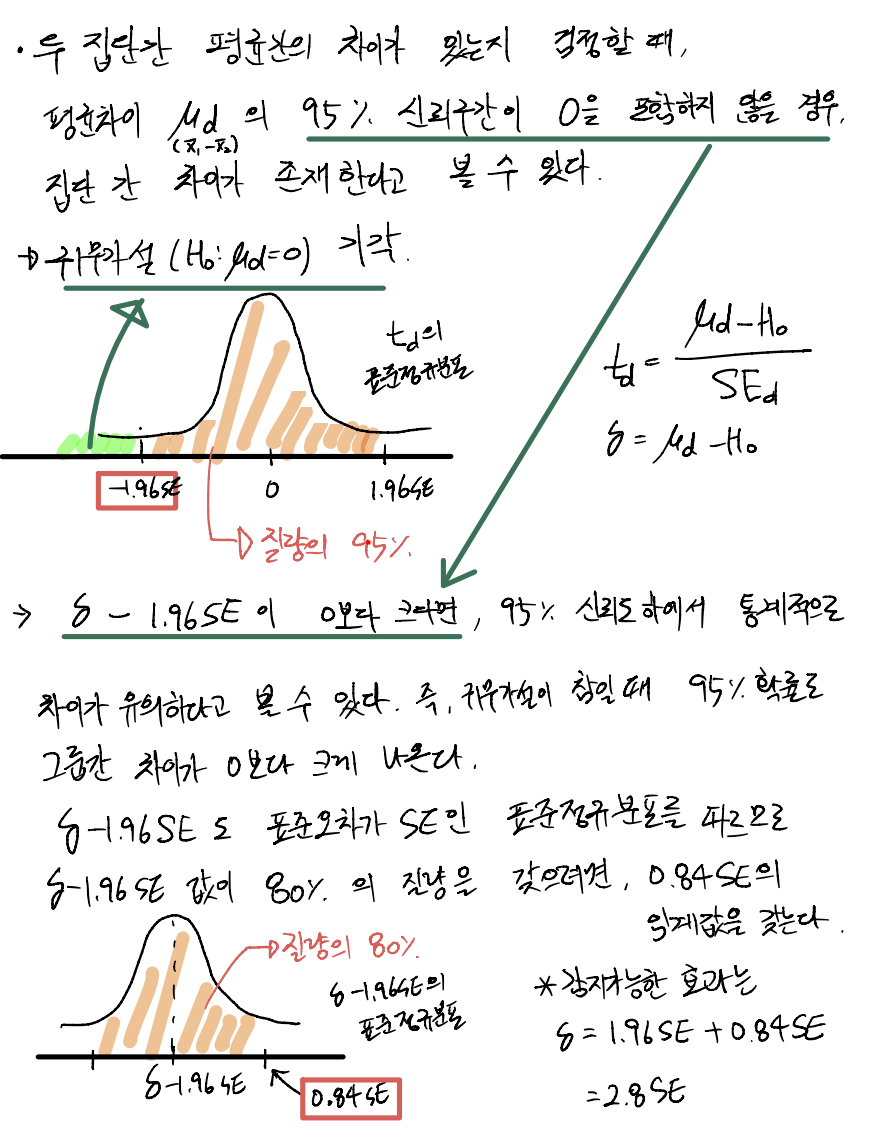
유의수준 5%일 경우, 5% 확률로 귀무가설을 잘못 기각하게 된다. 차이가 유의하다고 결론을 내리려면 매개변수 추정값과 귀무가설 사이의 차이인 δ가 최소한 0에서 1.96SE 만큼 떨어져 있어야 한다.
(δ-1.96SE가 95% 신뢰구간의 하한이기 때문이다. δ-1.96SE > 0 보다 크면 통계적으로 유의하다고 할 수 있다.)
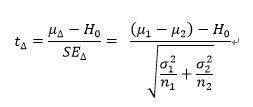
귀무가설을 올바르게 기각할 확률을 검정력이라고 한다.
검정력의 일반적인 기준은 80%로 설정하고, 귀무가설이 거짓일 때 80%의 확률로 귀무가설을 기각하는 것을 의미한다.
즉, 95% 신뢰구간의 하한이 0보다 높은 경우가 전체 실험의 80%에 달해야 한다.
δ-1.96SE 는 평균이 δ-1.96SE고 표준오차와 같은 분산을 갖는 정규분포입니다.
δ-1.96SE>0 인 경우가 80% 되려면(검정력의 80%), 차이가 0에서 1.96SE + 0.84SE만큼 떨어져야 한다. (1.96은 95% 신뢰구간을 확보하기 위한 값이고, 0.84는 신뢰구간의 하한이 0을 초과하는 경우가 전체의 80%에 해당하도록 하기 위한 값)
귀무가설과 관측된 추정값의 차이인 δ를 감지할 수 있어야 합니다.
유의수준(α) = 5%, 검정력(1-β) = 80% 라면, 감지 가능한 효과는 2.8SE = 1.96SE + 0.84SE
δ(8%) = 2.8SE를 감지한 표본크기를 확보해야함.
설계자 입장에서는 실험전이라 실험군의 표준오차를 알 수 없지만, 실험군과 대조군의 분산이 같을 것이라고 가정할 수 있다.
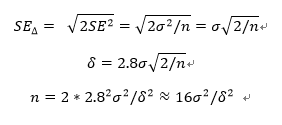
→ 대조군의 분산(σ^2)을 가장 타당한 추정값으로 사용해서 필요한 표본 크기를 정할 수 있다.
Summary#
인과추론의 목표는 데이터에서 인과추정량을 구하는 것
식별: 독립성 가정을 통해 관측할 수 없는 인과추정량을 추정할 수 있는 관측 가능한 통계량으로 만드는 것
무작위 통제 실험을 통해 처치와 잠재적 결과도 독립이게 만들 수 있음 (처치효과)
\[ E[Y_1-Y_0] = E[Y|T=1]-E[Y|T=0] \]추정: 식별을 통해 발생한 통계량을 활용해 추정 (표준오차, 신뢰구간, 그룹간 평균차이의 표준오차)
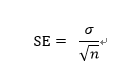
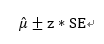
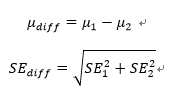
설계 시 표본크기 (유의수준(α) = 5%, 검정력(1-β) = 80%)
![Smart Causal Inference [SCI] - Home](../_static/qe-logo-large.png)