Chapter 1. 인과추론 소개#
작성자 : 박상호
1인당 초콜릿 소비량과 노벨상 수상자 수의 관계
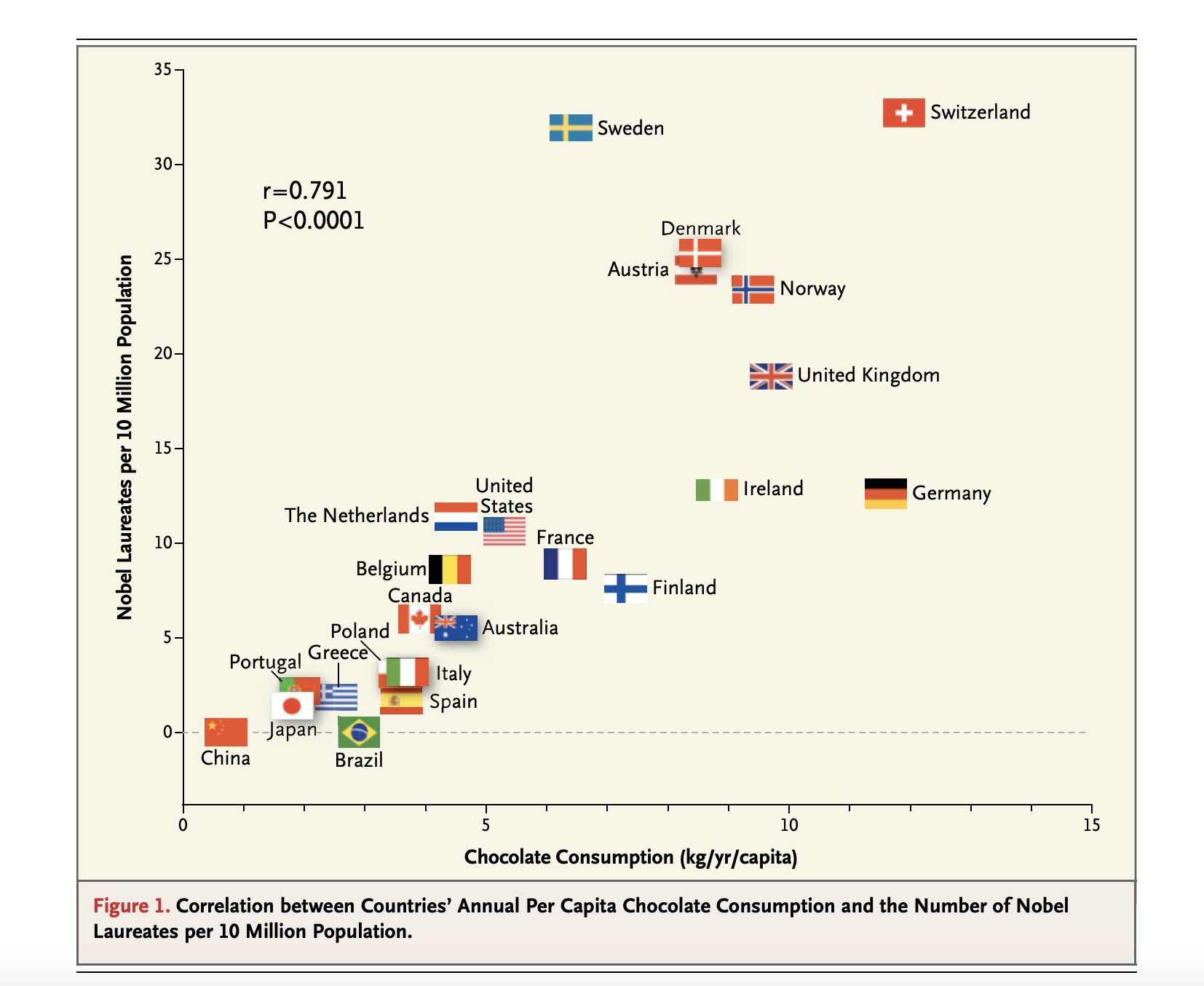
Messerli, F. H. (2012). Chocolate consumption, cognitive function, and Nobel laureates. N Engl J Med, 367(16), 1562-1564.
연관관계와 인과관계는 어떻게 다른가? 위의 1인당 초콜릿 소비량과 노벨상 수상자 수의 관계는 연관관계가 있다. 그러나 1인당 초콜릿 소비량이 많기 때문에 노벨상 수상자 수가 많다고 말하기 어렵다. 때로는 연관관계 중에서 인과관계를 이야기할 수 있는 경우가 있다. 언제 그럴까?
Potential outcome#
인과추론 문제에서는 풀리지 않는 문제가 있다. 한 사람이 특정 처치 \(T_i\)=t를 받았을 경우에는 t를 받지 않은 상황을 알 수가 없다. t를 받은 상황과 t를 받지 않은 상황을 비교하여야 인과추론을 할 수 있는데, 관찰 자료에서는 특정 처치 t를 받은 상황만 고려할 수 있다. t를 받은 상황과 t를 받지 않은 상황을 고려하기 위해서 다음과 같은 수식을 고려한다.
\(Y_{ti} = Y_i|do(T_i = t)\)
‘처치가 t인 상태일 때, 실험 대상 i의 결과는 Y가 될 것이다’라는 potential outcome을 정의한다.
\(Y_{1i}\) : 실험 대상 i가 처치 받은 잠재적 결과
\(Y_{0i}\) : 실험 대상 i가 처치 받지 않은 잠재적 결과
우리가 구하고자 하는 인과효과는 다음과 같다.
\(\tau_i = Y_{1i}-Y_{0i}\)
SUTVA 가정#
SUTVA는 stable unit of treatment value assumption을 의미한다. 이는 두 가지 의미를 함의한다. 첫째는 일치성(consistency)이고 둘째는 상호 간섭없음(no interference)이다.
일치성
\(T_i=t\)일 때 \(Y_i(t)=Y\)이다. 실험 계획 단계에서 고려한 T만 존재하여야 한다. 처치를 여러 번 했는데 한 번만 고려한 경우나 처치가 잘못 정의된 경우에는 일치성 가정이 위배될 수 있다.
상호 간섭없음
하나의 실험 대상에 대한 효과는 다른 실험 대상의 영향을 받지 않는다. 예를 들어, 백신의 경우에는 백신 접종률이 높아지면 다른 사람들이 해당 질병에 걸릴 확률이 낮아질 수 있다.
인과추정량과 편향#
가격할인이 개별 회사에 미치는 영향을 확인하기 위해 두 가지 잠재적 결과(\(AmountSold_{0i}\), \(AmountSold_{1i}\))를 확인하자. 가격할인이 판매량에 미치는 평균 영향은 추정할 수 있으므로 다음과 같은 인과 추정량을 고려하자.
평균처치효과 (average treatment effect)
\(ATE =E[AmountSold_{1i}-AmountSold_{0i}]\)
가격을 할인한 회사가 어떻게 판매량을 늘렸는지 알아보자.
실험군에 대한 평균 처치효과 (average treatment effect on the treated)
\(ATT =E[AmountSold_{1i}-AmountSold_{0i}|IsOnSales=1]\)
조건부 평균 처치효과(conditional average treatment effect)
크리스마스 주간의 할인 여부가 미치는 영향을 확인해보자.
\(CATE =E[AmountSold_{1i}-AmountSold_{0i}|weeksToXmas=0]\)
우리가 이론적으로 다음과 같은 potential outcome을 알 수 있다고 하자. 다음 표에서 \(i\)는 실험 대상, \(y\)는 관측한 결과, \(y_0\)과 \(y_1\)은 각각 실험군 및 대조군에 따른 잠재적 결과, \(t\)는 처치 여부, \(x\)는 크리스마스까지의 시간을 표시하는 공변량이다.
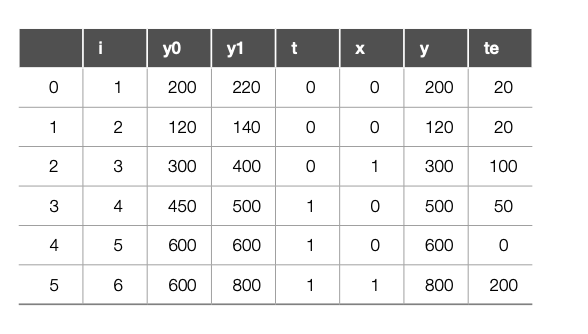
여기서 위에서 구한 \(ATE, ATT, CATE\)를 추정해보자.
\(ATE = (20+20+100+50+0+200)/6=65\)
가격할인으로 판매량이 평균 65개 증가한다. ATT는 \(T=1\)일 때 마지막 열의 평균이 된다.
\(ATT = (50+0+200)/3=83.33\)
크리스마스 1주일 전이라는 조건부 평균 효과(\(x=1\))는 회사 3번과 6번 효과의 평균에 해당한다.
\(CATE(x=1) = (100+200)/2=150\)
하지만, 실제 관측된 값과는 차이가 존재한다.
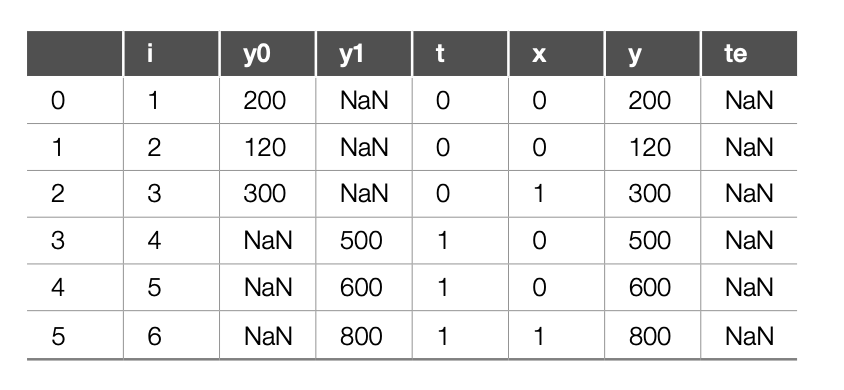
위의 표에서 관측된 값을 기반으로 계산해보자.
\(ATE = (500+600+800)/3-(200+120+300)/3=426.67\)
가격할인으로 판매량이 평균 427개 증가한다. ATT는 \(T=1\)일 때를 구하는 것이므로 \(E[AmountSold_{0i}|T=1]\)을 추정할 수가 없다.
\(ATT = E[AmountSold_{1i}-AmountSold_{0i}|IsOnSales=1]=E[AmountSold_{1i}|IsOnSales=1]=(800+600+500)/3=633.33\)
크리스마스 1주일 전이라는 조건부 평균 효과(\(x=1\))는 회사 3번과 6번 관측값의 차이에 해당한다.
\(CATE(x=1) = E[AmountSold_{1i}-AmountSold_{0i}|weeksToXmas=1]=800-300=500\)
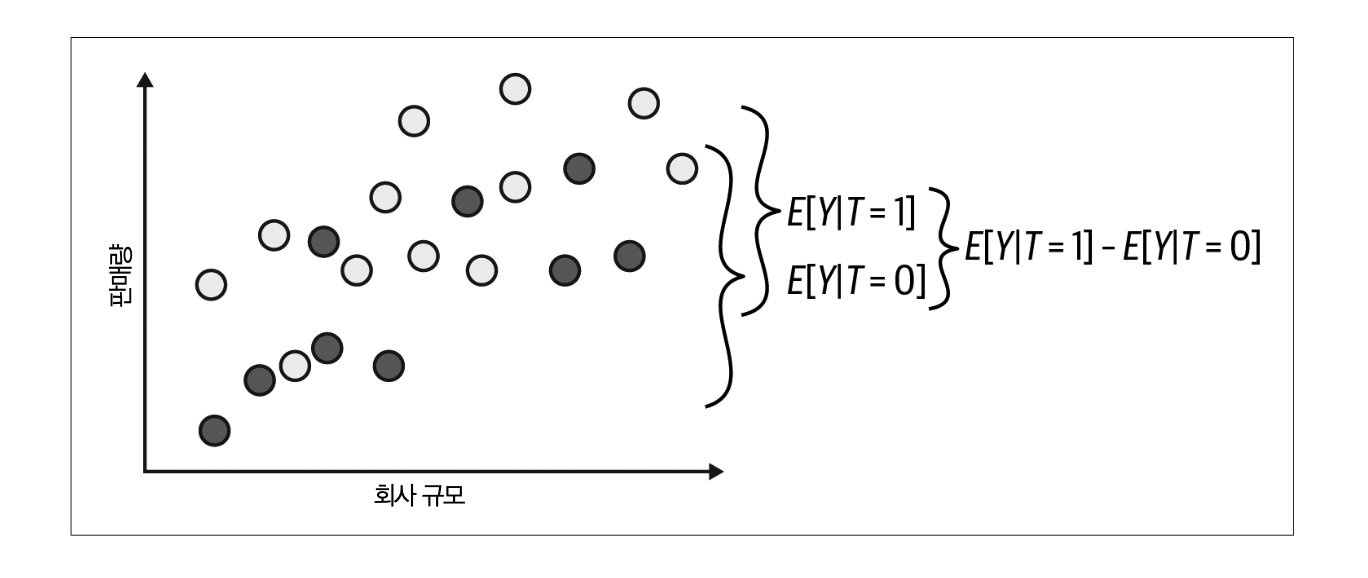
이론적인 결과값과 관측값은 큰 차이를 보인다. 이는 할인한 회사와 그렇지 않은 회사의 특성이 크게 다르기 때문이다. 실험군의 \(Y_0\)가 대조군보다 훨씬 높다. 인과관계와 연관관계를 다르게 만드는 요소인 편향에 대해 살펴보자. 편향을 수식적으로 다음과 같이 이해해보자. 할인 예제에서 처치와 결과 간의 연관관계는 다음과 같다.
\(E[Y|T=1]-E[Y|T=0]=E[Y_1|T=1]-E[Y_0|T=0]\)
\(=E[Y_1|T=1]-E[Y_0|T=1]+E[Y_0|T=1]-E[Y_0|T=0]\)
\(=E[Y_1-Y_0|T=1]+E[Y_0|T=1]-E[Y_0|T=0]\)
\(=ATT+편향\)
따라서,
\(E[Y_0|T=1]-E[Y_0|T=0]\)
이 두 군 사이의 편향에 해당한다. 두 군 사이에서는 할인 여부 외에도 수많은 변수가 차이가 있기 때문에 편향이 발생한다. 가격할인이 판매량에 미치는 영향을 파악하기 위해서는 할인한 회사와 하지 않는 회사가 평균적으로 비슷해야 한다. 따라서, 편향이 0이 되고, 실험군과 대조군이 처치에 유사하게 반응하면 평균의 차이가 평균 인과효과가 된다.
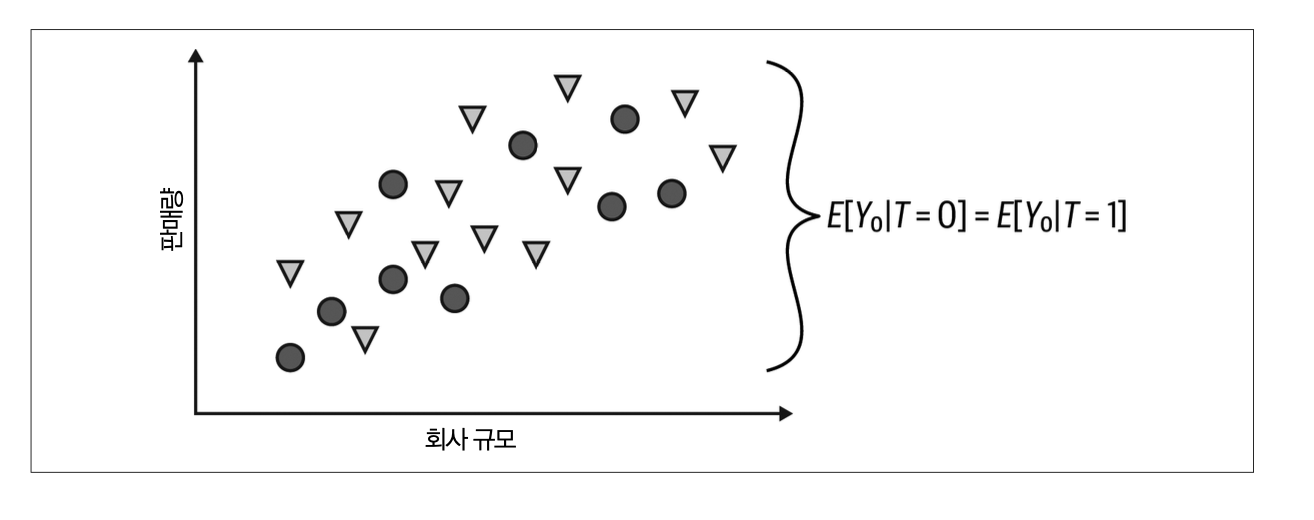
\(E[Y_1-Y_0|T=1]=E[Y_1-Y_0|T=0]\)
→ \(E[Y|T=1] - E[Y|T=0] = ATT = ATE = E[Y_1-Y_0]\)
실험군과 대조군이 서로 교환 가능하다면 인과추론을 할 수 있게 된다. 교환 가능성은 다음과 같은 수식으로 설명된다. 잠재적 결과가 처치와 독립적이다.
\((Y_0,Y_1)\perp T\)
잠재적 결과가 처치와 독립적인 상황을 만들기 위해서 randomization을 사용한다. 실험 대상에 처치를 무작위로 지정하게 되면, 실험 대상은 잠재적 결과는 물론이고 어떤 변수와도 독립적으로 된다. 무작위 대조 연구에서도 randomization이 중요한 요소인 이유이다.
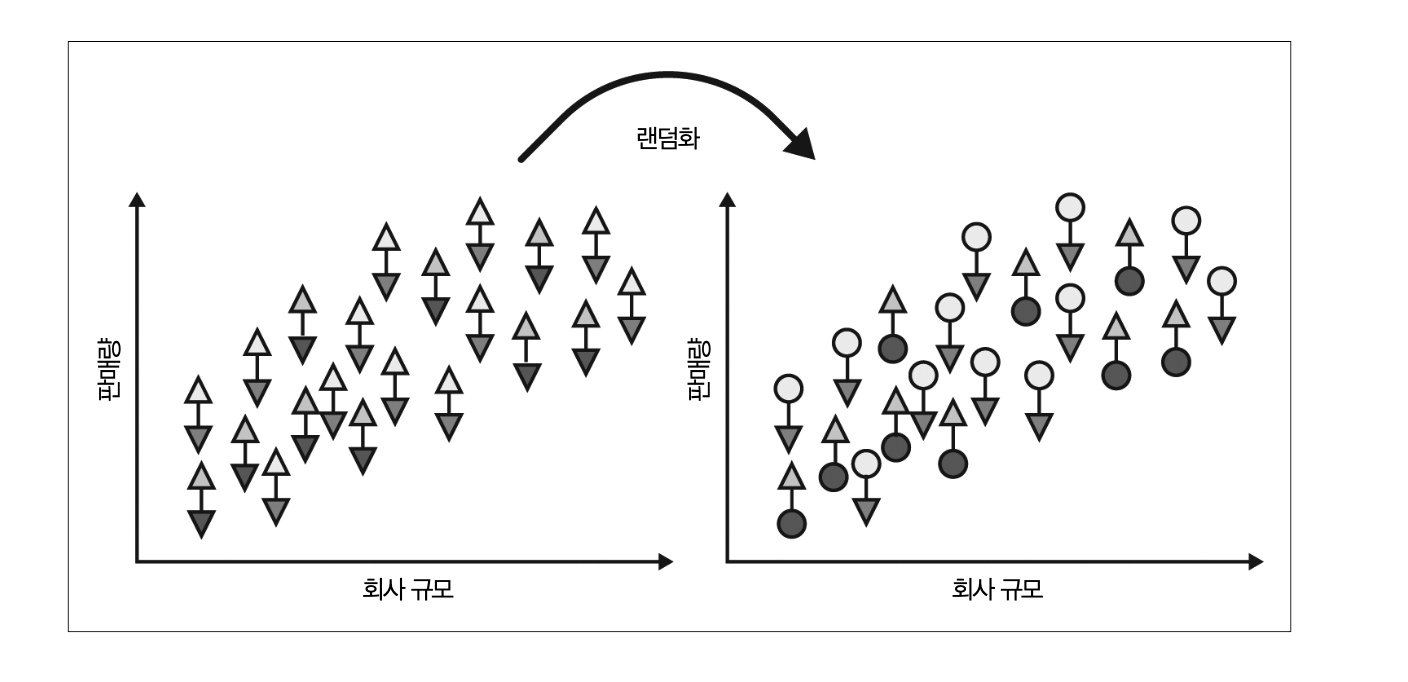
만약, \(Y_0\)만 관측할 수 있다면 다음과 같이 된다.
용어 설명#
식별 (identification) : 관측 가능한 데이터로 인과 추정량을 표현하는 방법을 알아내는 단계
추정 (estimation) : 실제로 데이터를 사용하여 앞서 식별한 인과 추정량을 추정하는 단계
인과적 식별 : 편향을 제거하고 실험군과 대조군을 비교할 수 있게 만드는 현명한 방법을 찾아내서 눈에 보이는 모든 차이를 처치에 따른 효과로 돌리도록 하는 과정
우리가 여기서 식별을 할 수 있는 이유는 데이터 생성 과정(처치 배정 메커니즘; 이 예시에서는 randomization)을 알거나 기꺼이 가정할 수 있기 때문이다.
요약#
Potential outcome
\((Y_0,Y_1)\perp T\)
\(E[Y|T=1] - E[Y|T=0] = ATT = ATE = E[Y_1-Y_0]\)
\(Y_i = (1-T_i)Y_{0i}+T_iY_{1i}\) (SUTVA 가정)
![Smart Causal Inference [SCI] - Home](../_static/qe-logo-large.png)