Chapter 7. 메타러너#

작성자 : 김혜민

들어가며#

  • 이질적 처치효과, 즉 실험 대상이 어떻게 처지에 따라 다르게 반응하는 지를 식별하는 데 중점을 둠

  • 이전 장에서 상호작용 항을 포함한 회귀분석을 사용하여 CATE 추정값을 구하는 방법을 살펴봄.

  • 이번 장에서는 몇 가지 머신러닝 알고리즘을 섞어서 CATE 추정을 진행

메타러너 (metalearner)#

  • 기존 예측 머신러닝 알고리즘을 활용하여 처치효과를 추정하는 간단한 방법

  • 메타러너를 ATE (처지의 평균 효과) 추정에 사용할 수 있지만, 일반적으로 고차원 데이터를 잘 처리하기 때문에 주로 CATE (조건부 처지 평균 효과) 사용함

  • 메타러너는 사용하는 머신러닝 방법에 크게 좌우됨 → 여러 방법을 시도해보고 가장 효과적인 것을 확인

  • ATE : 처지의 평균적인 효과

  • CATE : 조건부 처지 효과

    • 개인마다 각각 어떤식으로 작동할지?

    • 관찰된 공번량(X)에 대한 조건부 처리 효과

\[ (CATE, τ(x)= E[D|X=x] = E[Y(1)-Y(0)|X=x]) \]

1. 이산형 처치 메타러너#

➡️ 가정

  • 온라인 소매업체의 마케팅 팀에서 근무

  • 마케팅 이메일을 통하여 클릭 전환율 상승

  • 어떤 고객이 마케팅 이메일을 잘 받는지 파악하는 것이 중요

이 문제를 해결하기 위해서 이메일이 고객의 미래 구매량에 미치는 조건부 평균 처지효과를 추정하려고 함

CATE 추정값을 바탕으로 누구에게 메일을 발송하면 효율적일지 전략 수립 가능

T : 이메일 발송 여부 mkt_email

Y : 한달 후 구매 금액 next_month_pv

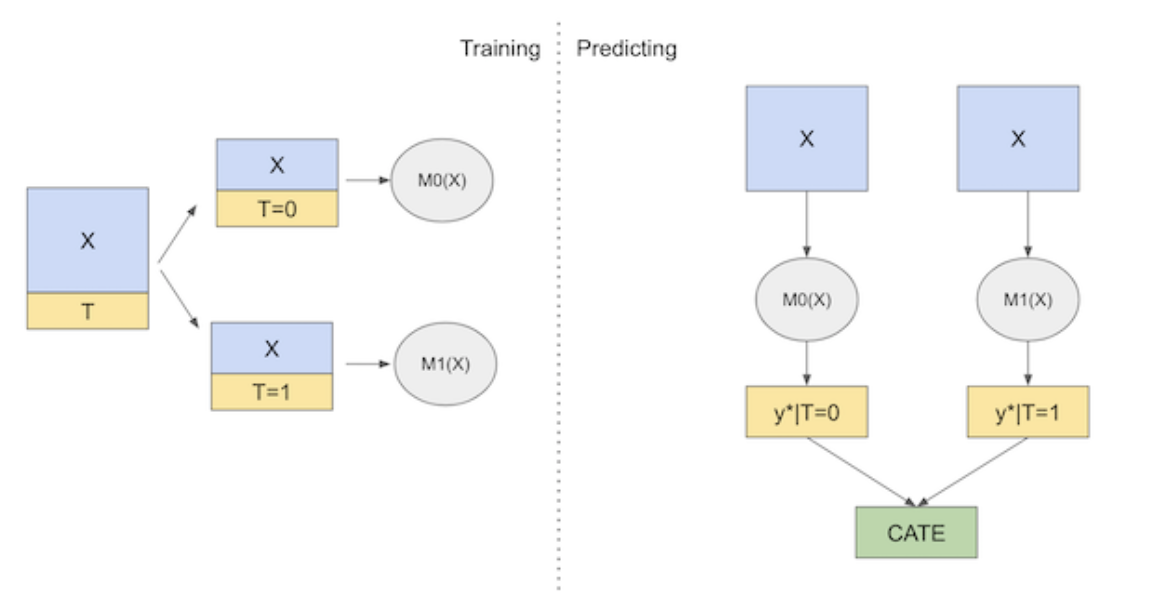
1-1. T 러너#

통제, 처리 그룹을 각각 다른 모형으로 학습, 두 차이로 CATE를 추정

#. 추정 방법#

Step1 : 처치를 받지 않은 개체와 처리를 받은 개체를 각각 다른 모형을 사용해서 학습

\[ μ_0(x) = E[Y|T=0,X]\]
\[ μ_1(x) = E[Y|T=1,X]\]

Step2 : 이 두 그룹의 차이로 CATE를 추정

\[ \hat{τ}(x)_i = \hat{μ_1}(X_i) — \hat{μ_0}(X_i)\]

  • T 러너가 T = 0, T=1 에서 각자 머신러닝 모델을 학습

  • 예측 시점에 두 모델을 모두 사용해서 실험군과 대조군 차이를 추정

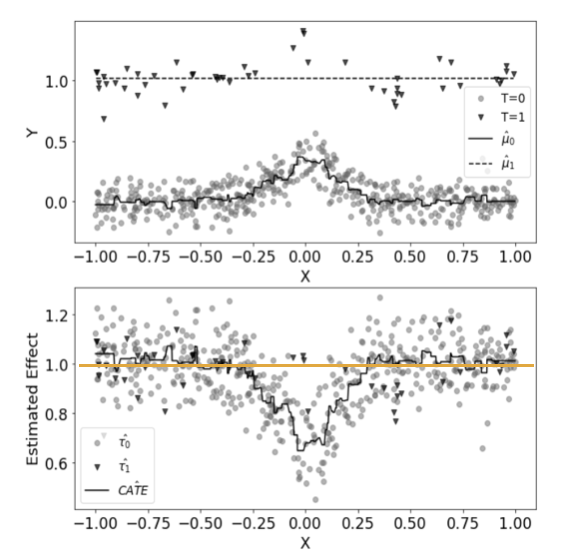
상대 누적 이득 곡선 AUC : 처치효과 높은 - 낮은 순서대로 올바르게 정렬했는 지를 확인

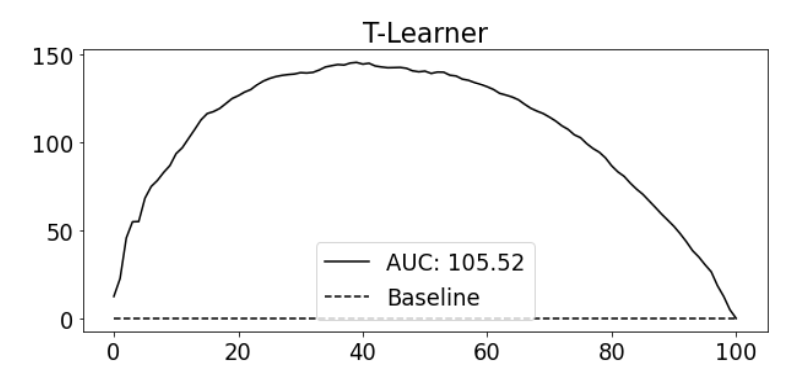
상대 누적 이득 곡선 AUC : 처치효과 높은 - 낮은 순서대로 올바르게 정렬했는 지를 확인

한계점 : 정규화 편향

  • 대조군은 많고 실험군은 적은 상황

    • 과적합을 피하기 위해 모델이 단순해질 수 있음

  • 실제 해당 데이터 CATE = 1 이 나와야 함

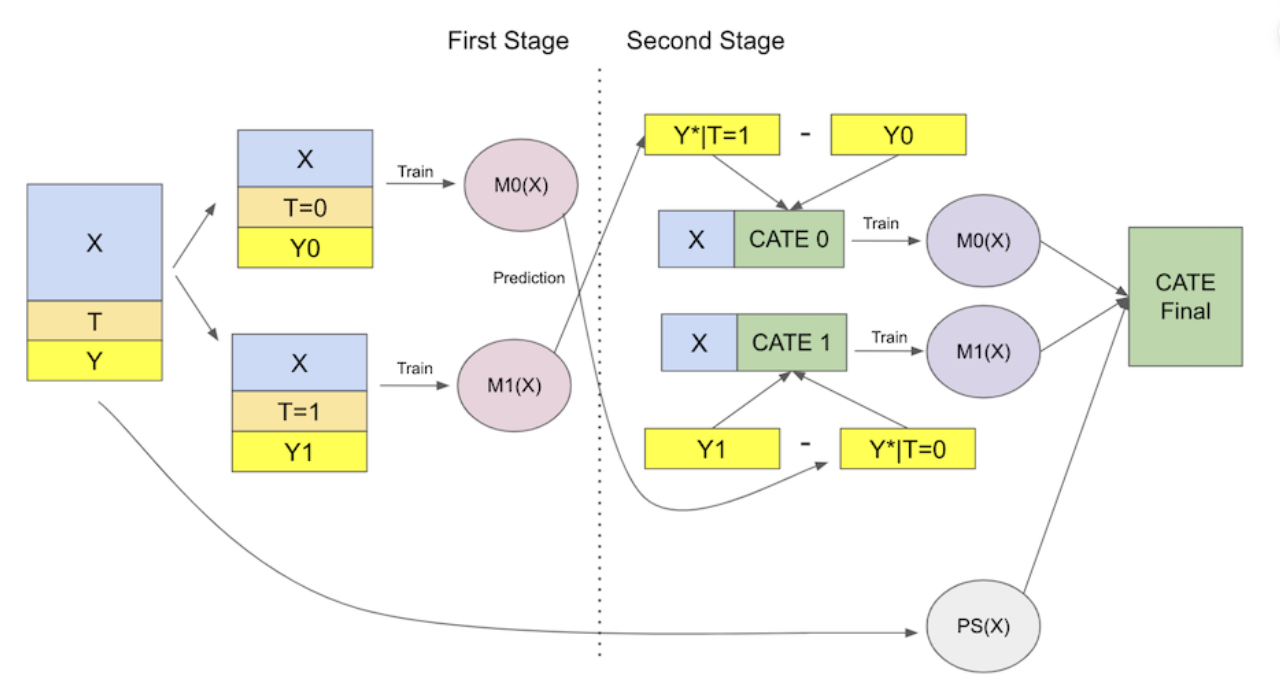
1-2. X 러너#

통제, 처리 그룹을 각각 다른 모형을 사용하여 학습하고, 해당 모형을 활용하여 각 그룹의 개별 처치 효과를 추정

개별 처지 효과에 가중치를 적용하여 최종 결과값 도출

두 집단의 데이터 양 차이가 많을 때 용이

#. 추정 방법#

Step1 : 처치를 받지 않은 개체와 처리를 받은 개체를 각각 다른 모형을 사용해서 학습

\[ \hat{μ_0}(x) ≈ E[Y|T=0,X]\]
\[ \hat{μ_1}(x) ≈ E[Y|T=1,X]\]

Step2: 통제그룹, 처리 그룹의 개별 치료 효과 추정

  1. 통제 그룹의 개별 치료 효과 추정

\[ \hat{τ}(X,T=0)=\hat{μ}_1(X,T=0)−Y_{T=0}\]

  • \(μ_1(X,T=0)\)는 통제 그룹의 데이터 X를 사용하여 처리 그룹 모델 \(\hat{μ}_1\)이 예측한 결과입니다.

  • YT=0Y_{T=0}YT=0는 실제로 처리를 받지 않은 통제 그룹의 결과입니다.

  • 이 차이는 “통제 그룹이 실제로는 처리를 받지 않았지만, 처리를 받았더라면 얻었을 결과”를 나타냅니다.

  1. 처리 그룹의 개별 치료 효과 추정

\[ \hat{τ}(X,T=1)=Y_{T=1}−\hat{μ}_0(X,T=1)\]

**** 매우 작은 표본에 적합된 를 사용할 경우 위에 해당하는 결과값들이 잘못될 가능성이 큼

**** 매우 작은 표본에 적합된 \(\hat{μ}_1\)를 사용할 경우 위에 해당하는 결과값들이 잘못될 가능성이 큼

  • 한 모델을 처치효과를 잘못 대체했기 떄문에 부정확하고

  • 다른 하나의 모델은 그 값을 올바르게 대체했으므로 정확함

⇒ 두 모델을 정확한 모델에 더 많은 가중치를 부여하여 결합!

Step 3: 가중치 적용 및 최종 개별 치료 효과 추정

\[ \hat{τ}(x)=\hat{μ}(X)_{τ0}\hat{e}(x)+\hat{μ}(X)_{τ1}(1−\hat{e}(x)) \]

  • \(\hat{e}(x)\)는 성향 점수, 개체가 처리 그룹에 속할 확률을 나타냄

  • 일반적으로 성향점수를 사용한 이 가중평균은 더 많은 데이터를 사용하여 학습된 \(\hatμ_t\)모델에서 얻은 처치효과 추정값에 더 많은 가중치는 부여

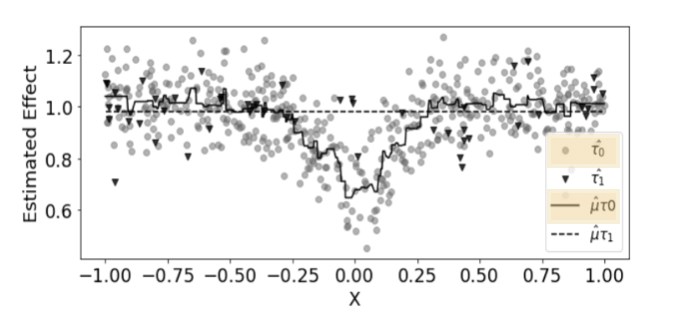
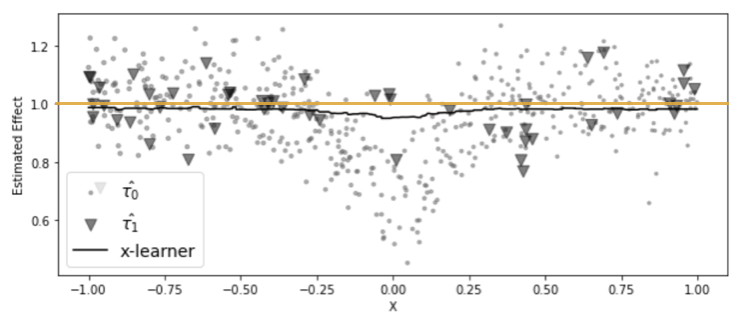
  • T러너에 비해 잘못 추정된 CATE를 보정하는 것에 더 좋은 성능

  • 일반적으로 한 실험 대상의 집단이 다른 집단보다 훨씬 클 떄 X러너의 성능이 좋음

2. 연속형 처지 메타러너#

연속성 처치의 경우 메타러너를 적용하기 까다로울 수 있음

➡️ 가정

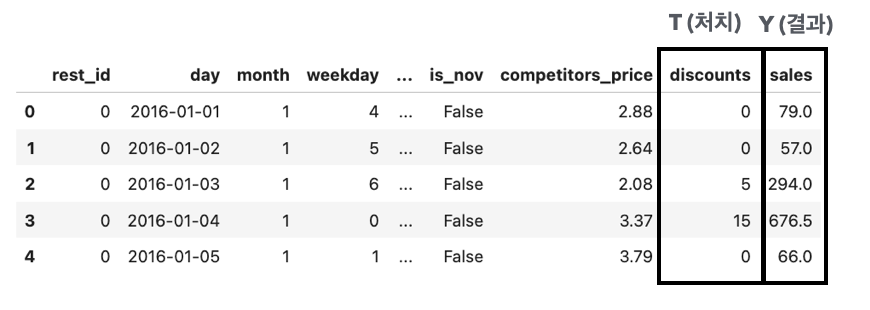
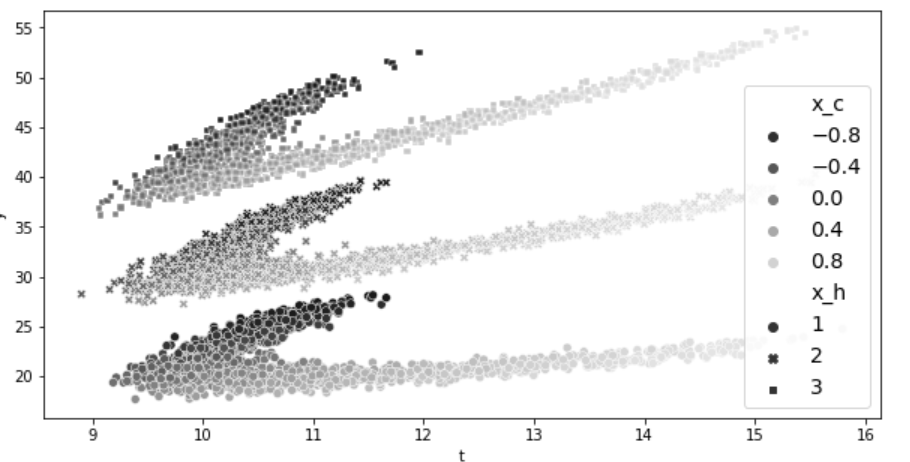
  • 레스토랑 할인 정보 데이터

  • 어느 시점에 할인을 제공하면 더 좋은 매출을 발생시키는 지 궁금

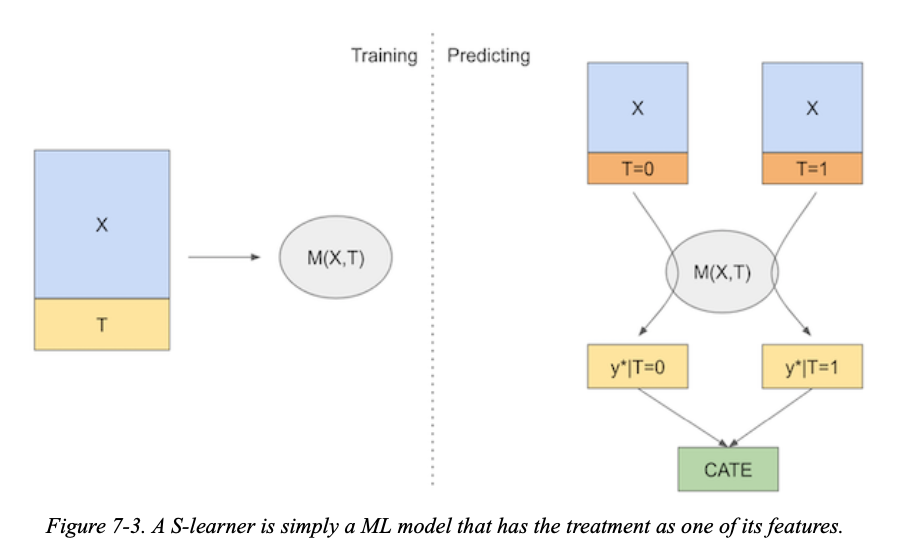
2-1. S 러너#

단일(Single) 머신 러닝 모델을 사용하여 결과를 예측

\[ {μ}(x) = E[Y|T,X]\]

공변량 X와 처리 변수 T를 모두 모델의 특성으로 포함 → 이 방법은 반사실적 예측을 직접 출력하여 CATE 추정

  • 이산형 처치에서도 사용가능

\[ \hat{τ}(x)_i = \hat{μ}_s(X_i, T=1) — \hat{μ}_s(X_i, T=0)\]

#. 추정 방법#

Step1 : 단일 머신 러닝 모델( \(μ_s\)) 을 X, T를 사용하여 학습

\[ μ(x,t)=E[Y∣T=t,X=x] \]
\[ \hat{Y}^=\hat{β}_0+\hat{β}_1T+\hat{β}_2X \]

Step2: 반사실적 예측 (실제로 일어나지 않은 상황에서의 결과를 예측)

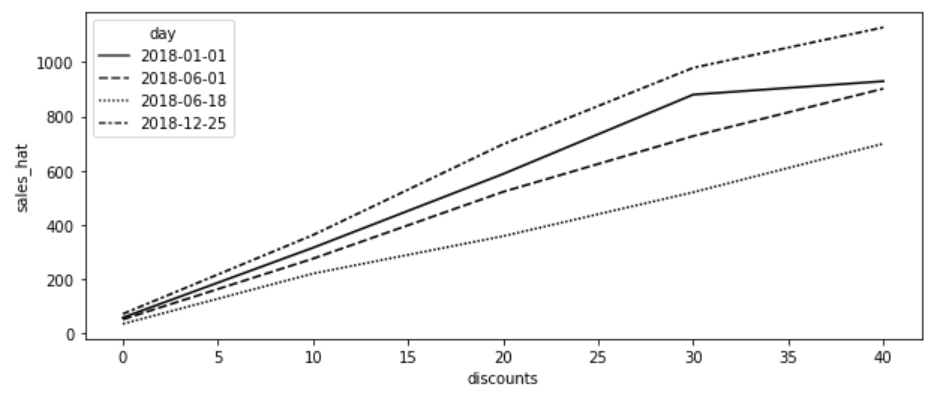
  • 데이터 확장 : 연속성 처치의 경우 처치의 그리드 정의(해당 예제에서는 0~40% 이므로 10단위로 범주 주여)

  • \(μ_s\) 를 사용하여 확장된 데이터에서 반사실적 결과 예측

해당 그래프에서 2018-12-25에 추정된 반응 함수가 2018-06-18일보다 더 가파른 모습을 보여줌

→ 고객이 크리스마스에 할인에 더 민감함을 모델이 학습했다는 의미

Step3: CATE 추정

  • 기울기 매개변수는 각 처지 값에 해당하는 결과의 변화율을 나타냄

  • 이러한 기울기 매개변수의 차이를 통해 조건부 평균 치료 효과(CATE)를 추정

    • 단순선형회귀 계수 공식 활용

      \[ \hat{β} = Cov(t,y) / Var(t) \]

  • T=1 일 때 \(\hat{Y}_1 = \hat{β}_0 + \hat{β}_1​⋅1 + \hat{β}_2X\)

  • T=0 일 때 \(\hat{Y}_0 = \hat{β}_0 + \hat{β}_1​⋅0 + \hat{β}_2X\)

  • CATE 계산

    \(CATE(X) = \hat{Y}_1 - \hat(Y)_0 = (\hat{β}_0 + \hat{β}_1⋅1 + \hat{β}_2X) - (\hat{β}_0 + \hat{β}_1⋅0 + \hat{β}_2X) = \hat{β}_1\)

한계점

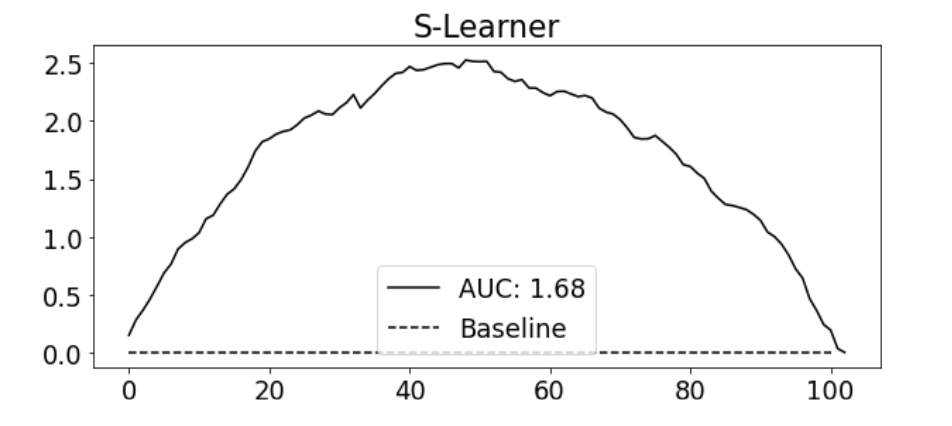
  • 누적 이득 곡선에서 보면 S러너는 간단하지만 괜찮은 성능을 보여주는 것처럼 보임

  • S 러너는 랜덤화된 데이터가 많고 상대적으로 쉬운 데이터셋에 특화된 성능

  • 큰 단점으로 처치효과를 0으로 편향시키려는 경향 존재

    • 일반적으로 정규화 머신러닝 모델을 사용 → 정규화는 추정된 처치효과를 제한할 수 있음

  • 처치변수가 다른 공변량보다 결과를 설명하는 데 영향력이 매우 적다면, S러너는 처치변수를 완전히 버릴 수 있음

이러한 ATE 편향문제를 해결하는 방법으로 이중/편향 제거 머신러닝 (R 러너)를 활용

2-2. 이중/편향 제거 머신러닝 (= R 러너)#

결과와 처치의 잔차를 구성할 때 머신러닝 모델을 사용

  • 복잡한 함수 형태 포착 가능 → 과적합 가능성 있음

\[ Y_i -\hat{μ}_y(X_i) = τ⋅(T_i - \hat{μ}_i(X_i)) + ϵ_i \]

#. 주요개념#

  1. 결과 Y 추정 (머신러닝 회귀 모델 \({μ}_y\) 사용)

  2. 처치 T 추정 (머신러닝 회귀 모델 \({μ}_t\) 사용)

  3. 잔차 계산

    • 결과 잔차 : \(\tilde{Y} = Y−μ_y(X)\)

    • 처지 잔차 : \(\tilde{T} = T−μ_t(X)\)

  4. 결과의 잔차를 처치의 잔차에 회귀

    \(\tilde{Y} = τ\tilde{T} + ϵ\)

    • τ : 추정하려고자 하는 처치 효과 : ATE에 해당

    \[ ⁍ \]

문제점 : 과적합

→ k fold 교차 검증에서 잔차를 얻는 방법으로 해당 문제를 완화 시킬 수 있음

K-1 모델 추정, 남겨진 폴드에서 잔차를 얻음 * K번 반복

의도적으로 잔차를 0으로 만들지 않음

#. CATE 추정#

\[ Y_i -\hat{μ}_y(X_i) = τ(X_i)⋅(T_i - \hat{μ}_i(X_i)) + ϵ_i \]
\[ \tilde{Y} = τ(X_i)\tilde{T} + ϵ \]

  • 오차 관련 식으로 조정 → 인과 손실 함수

    \[ ⁍ \]

  • 손실의 제곱을 최소화하면 원하는 CATE \(τ(X_i)\) 의 기댓값을 추정 가능

    \[ τ(X_i) = \tilde{Y} /\tilde{T} + ϵ \]
    \[ \hat{L}_n(τ(x)) =1/n∑[(Y_i-\hat{M}_y(X_i)) - τ(X_i)(T_i-\hat{M}_t(X_i))] \]

    R러너가 최소하하려는 손실이므로 R 손실이라고도 부름

    \[ ⁍ \]

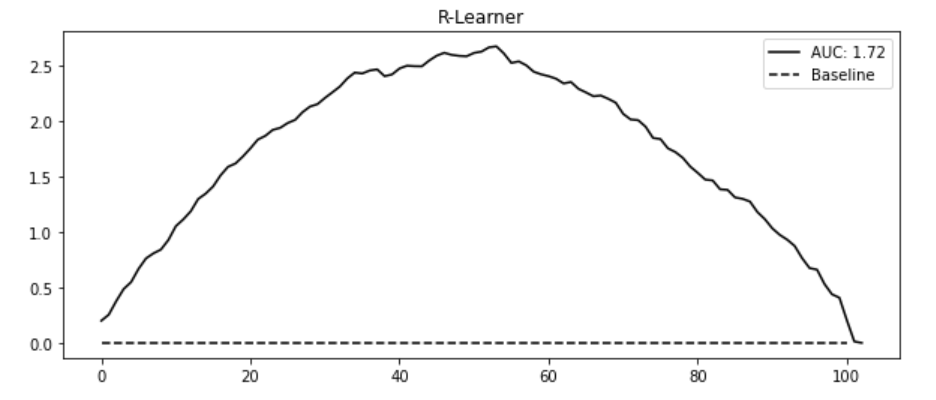
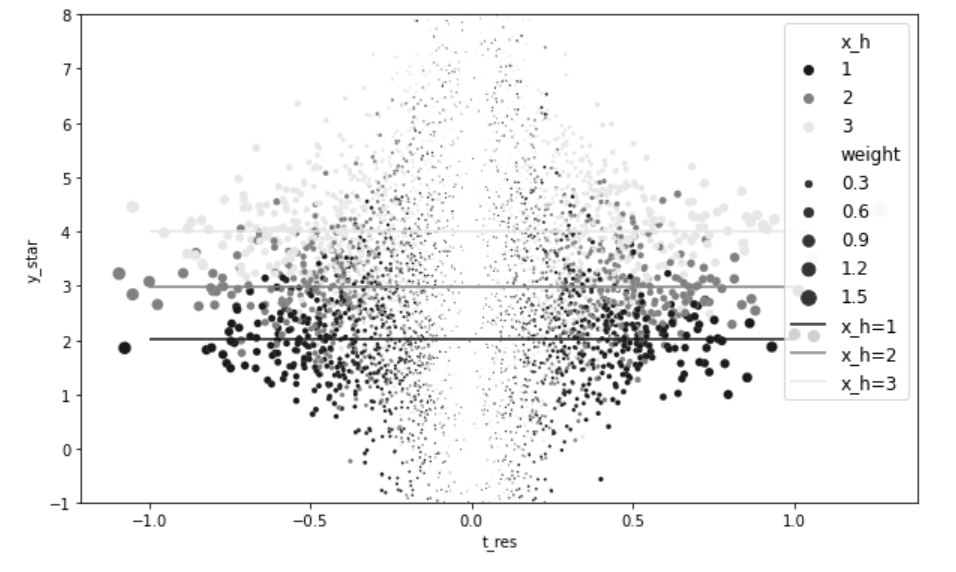
  • 시각화

요약#

이산형

  1. T-러너

    • 두 개의 모델을 각각 학습하고 차이로 처리 효과를 추정

    • 정규화 편향이 발생하기 쉬움

  2. X-러너

    • 두 개의 모델을 각각 학습

    • 각 그룹의 개별 치료효과 추정 후 성향점수로 가중치 부여 (작은 표본 학습 모델의 의존도 낮추기 위함)

    • 일반적으로 한 실험 대상의 집단이 다른 집단보다 훨씬 클 때 X러너의 성능이 좋음

연속형

  1. S-러너

    • 단일 모델 학습

    • 처지값의 그리드를 주어 반사실 예측에 모델 사용

    • 기울기 매개변수를 추정

  2. 이중 머신러닝

    • 결과 모델, 처치 모델 추정

    • 각각의 잔차 추정

    • 과적합 해결 위해 k fold 교차 검증에서 잔차를 얻는 방법 사용